当前位置：首页 > 行业动态 > 正文

反向传递神经网络

admin
行业动态
2025-05-03
2

反向传递神经网络即反向传播算法，通过误差反向逐层调整权值，实现

原理、实现与优化

核心概念与基本原理

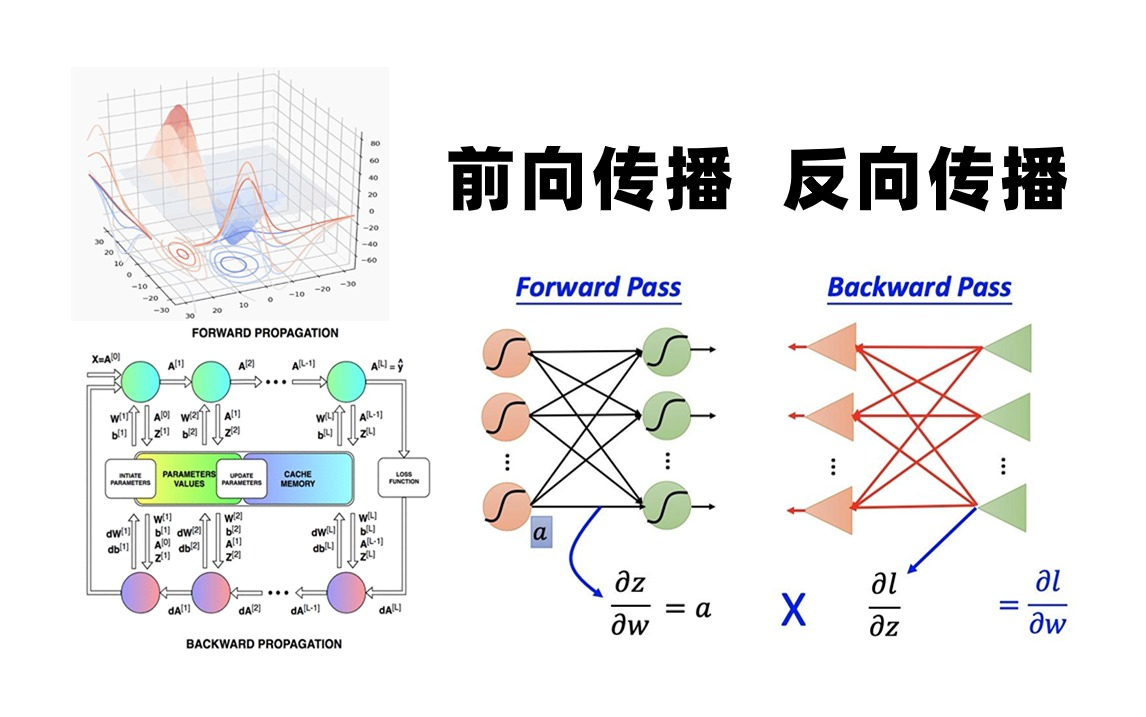
反向传递神经网络（Backpropagation Neural Network）是深度学习的核心算法，其本质是通过梯度下降法优化神经网络参数,该算法由前向传播和反向传播两个阶段构成：

阶段	核心目标	数据流向
前向传播	计算预测值与损失函数	输入→隐藏层→输出
反向传播	计算梯度并更新网络参数	输出→隐藏层→输入

关键特性：

端到端训练：通过链式法则自动计算各层梯度
参数共享：同一层的神经元共享权重参数
误差反向流动：从输出层逐层向前传播误差信号

数学推导与计算流程

以三层神经网络（输入层-隐藏层-输出层）为例：

前向传播公式：

反向传递神经网络第1张

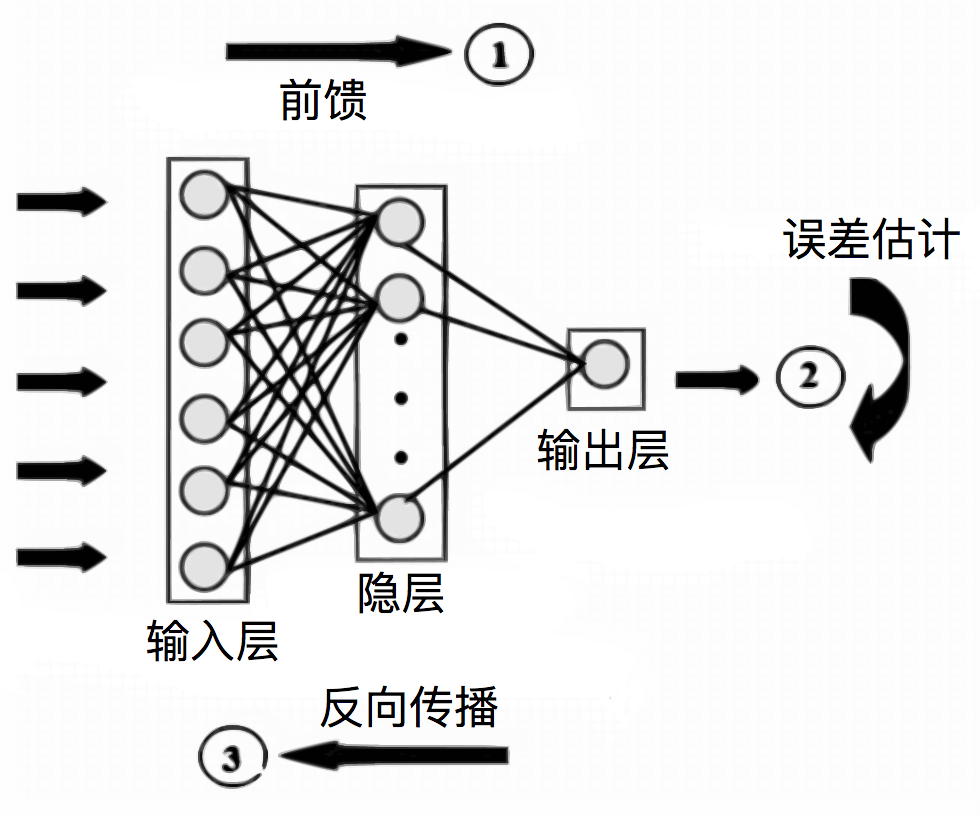
隐藏层输入：$z_h = W_1X + b_1$
隐藏层输出：$a_h = sigma(z_h)$（$sigma$为激活函数）
输出层输入：$z_o = W_2a_h + b_2$
输出层预测：$hat{y} = sigma(z_o)$

损失函数：
常用均方误差（MSE）：$L = frac{1}{2}sum(hat{y}-y)^2$

反向传播梯度计算：

输出层误差：$delta_o = hat{y} y$
隐藏层误差：$delta_h = (W_2^Tdelta_o) odot sigma'(z_h)$
权重梯度：
- $dW_2 = a_h^Tdelta_o$
- $dW_1 = X^Tdelta_h$
偏置梯度：
- $db_2 = delta_o$
- $db_1 = delta_h$

参数更新：
采用随机梯度下降（SGD）：
$$
W leftarrow W eta cdot dW
b leftarrow b eta cdot db
$$
（$eta$为学习率）

算法实现步骤

# 伪代码示例（单样本更新）
def backpropagation(X, y, W1, b1, W2, b2, learning_rate):
    # 前向传播
    z1 = X@W1 + b1
    a1 = relu(z1)
    z2 = a1@W2 + b2
    predict = sigmoid(z2)
    # 计算损失
    loss = mse_loss(predict, y)
    # 反向传播
    delta2 = predict y
    delta1 = (delta2@W2.T)  relu_derivative(z1)
    # 梯度计算
    dW2 = a1.T@delta2
    db2 = np.sum(delta2, axis=0)
    dW1 = X.T@delta1
    db1 = np.sum(delta1, axis=0)
    # 参数更新
    W2 -= learning_rate  dW2
    b2 -= learning_rate  db2
    W1 -= learning_rate  dW1
    b1 -= learning_rate  db1
    return W1, b1, W2, b2, loss

关键优化技术

优化方法	作用机制
动量法（Momentum）	引入历史梯度累积项，加速收敛并抑制振荡
RMSProp	自适应调整学习率，解决不同参数梯度量级差异问题
Adam优化器	结合动量与RMSProp，同时进行梯度修正和学习率自适应
批标准化（BatchNorm）	对每层输入进行标准化，缓解内部协变量偏移问题
残差连接	通过跳跃连接解决梯度消失问题，支持超深网络训练

典型问题与解决方案

梯度消失/爆炸：

原因：非线性激活函数导致梯度指数级衰减（如Sigmoid/Tanh）
解决方案：
- 使用ReLU系激活函数（如Leaky ReLU）
- 梯度裁剪（Gradient Clipping）
- 权重初始化策略（如He/Xavier初始化）

局部最优解：

现象：损失函数陷入鞍点或次优极值
应对措施：
- 多次随机初始化训练
- 模拟退火策略
- 集成多个模型结果（Bagging）

应用实践建议

场景需求	配置建议
图像分类任务	卷积层+全连接层，ReLU激活，Adam优化器，交叉熵损失
时序预测问题	LSTM/GRU网络，tanh激活，早停法防止过拟合
强化学习环境	结合Q-learning，使用经验回放缓冲区，优先采样重要样本
生成对抗网络（GAN）	交替训练生成器与判别器，使用Wasserstein距离改进训练稳定性