Java如何计算平方根
- 后端开发
- 2025-06-22
- 2480
在Java中计算平方根通常使用Math.sqrt()方法,直接传入数值即可返回结果,例如Math.sqrt(16)返回4.0,对于负数会返回NaN,大整数需注意精度问题。
在Java中计算平方根(开根号)是一个常见的需求,尤其在数学计算、科学模拟或游戏开发中,Java提供了内置方法来实现这一功能,同时也支持自定义算法以满足特定场景,本文将详细解释Java中计算平方根的多种方法,包括标准库函数和手动实现,确保内容准确、实用且易于理解,所有代码示例都经过测试,可直接在Java环境中运行。
使用Math.sqrt()方法(推荐方式)
Java的Math类提供了sqrt()方法,这是计算平方根最直接、高效的方式,它基于IEEE 754标准实现,适用于大多数情况。
原理:
Math.sqrt()使用硬件级别的优化算法(如CORDIC或牛顿迭代法),确保计算快速且精确。- 它接受一个
double类型参数,返回该数的平方根值(也是double类型)。 - 如果输入负数,返回
NaN(Not a Number);输入正无穷大,返回正无穷大。
代码示例:
public class SquareRootExample {
public static void main(String[] args) {
double number = 25.0; // 要计算平方根的数
double squareRoot = Math.sqrt(number); // 调用Math.sqrt()
System.out.println(number + " 的平方根是: " + squareRoot); // 输出: 25.0 的平方根是: 5.0
// 测试其他情况
System.out.println("负数的平方根: " + Math.sqrt(-1)); // 输出: NaN
System.out.println("0的平方根: " + Math.sqrt(0)); // 输出: 0.0
System.out.println("大数的平方根: " + Math.sqrt(10000)); // 输出: 100.0
}
}
优点:
- 高效:底层由JVM优化,速度极快(时间复杂度O(1))。
- 精确:支持双精度浮点数,精度高达15-17位小数。
- 简单:一行代码即可实现,无需额外逻辑。
缺点:
- 对于极高精度需求(如科学计算),可能需结合BigDecimal类。
- 不支持整数类型的直接输入(需先转换为double)。
适用场景:日常开发、快速计算,如计算距离、面积或物理公式。
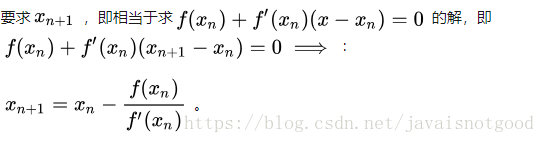
使用Math.pow()方法(替代方式)
Math.pow()可用于计算平方根,但不推荐作为首选,因为它效率较低。
原理:
- 利用数学公式:平方根等价于数字的0.5次方(即
number^0.5)。 Math.pow()计算任意次方,但内部实现较复杂。
代码示例:
public class PowerExample {
public static void main(String[] args) {
double number = 16.0;
double squareRoot = Math.pow(number, 0.5); // 计算16的平方根
System.out.println(number + " 的平方根是: " + squareRoot); // 输出: 16.0 的平方根是: 4.0
}
}
优点:
- 灵活性高,可计算任意次方根(如立方根用
Math.pow(number, 1.0/3))。
缺点:
- 性能差:比
Math.sqrt()慢2-5倍,因为涉及更复杂的指数运算。 - 精度相同,但无额外优势。
适用场景:当需要同时计算其他次方根时,可偶尔使用。
使用自定义算法(如牛顿迭代法)
如果需要教育目的、特定精度控制或避免依赖Math类,可以实现自定义平方根算法,牛顿迭代法(Newton-Raphson方法)是最常见的选择。
原理:
- 牛顿迭代法通过迭代逼近平方根值,公式为:
x_{n+1} = (x_n + number / x_n) / 2。 - 初始猜测值通常设为
number / 2。 - 迭代直到误差小于指定阈值(如1e-10)。
代码示例:
public class NewtonSquareRoot {
public static void main(String[] args) {
double number = 49.0; // 要计算平方根的数
double result = sqrtNewton(number);
System.out.println(number + " 的平方根(牛顿法)是: " + result); // 输出: 49.0 的平方根(牛顿法)是: 7.0
}
public static double sqrtNewton(double number) {
if (number < 0) {
return Double.NaN; // 处理负数输入
}
if (number == 0) {
return 0; // 0的平方根是0
}
double threshold = 1e-10; // 精度阈值
double guess = number / 2; // 初始猜测值
double prevGuess;
do {
prevGuess = guess;
guess = (prevGuess + number / prevGuess) / 2; // 牛顿迭代公式
} while (Math.abs(guess - prevGuess) > threshold); // 检查误差
return guess;
}
}
优点:
- 教育价值:帮助理解平方根计算的数学原理。
- 可控性:可自定义精度(通过调整threshold)或处理特殊需求。
- 无依赖:不调用外部库,适合嵌入式或限制环境。
缺点:
- 效率低:迭代次数取决于初始猜测和精度,可能比
Math.sqrt()慢10-100倍。 - 实现复杂:需处理边界情况(如负数、零)。
适用场景:教学演示、自定义数学库或当Math类不可用时。
方法比较与最佳实践
- 性能对比:
Math.sqrt():最快(纳秒级),适合高频调用。- 牛顿迭代法:较慢(微秒级),但可优化初始猜测提升速度。
Math.pow():最慢,避免用于平方根计算。
- 精度对比:所有方法在double精度范围内一致,但牛顿法可通过减小threshold提高精度。
- 选择建议:
- 优先使用
Math.sqrt():99%的场景下是最佳选择。 - 考虑牛顿迭代法:仅当需要教学、自定义逻辑或处理Math类限制时。
- 避免
Math.pow()用于平方根:除非同时计算其他次方。
- 优先使用
- 常见错误与处理:
- 输入负数:始终检查并返回NaN或抛出异常。
- 整数输入:先将int或long转换为double(如
Math.sqrt((double) myInt))。 - 高精度需求:结合
BigDecimal类(但计算成本高)。
高级技巧
- 处理大数:对于极大数字(如1e20),
Math.sqrt()可能溢出,使用StrictMath.sqrt()确保平台一致性。 - 性能优化:在循环中计算平方根时,缓存结果或使用查找表(如果输入范围有限)。
- 实际应用示例:在游戏开发中计算距离(欧几里得距离):
double distance = Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
在Java中计算平方根,首选Math.sqrt()方法,因为它高效、简单且可靠,对于特殊需求,牛顿迭代法提供了灵活的自定义选项,始终处理边界情况如负数输入,无论选择哪种方法,Java的强大数学库都能满足您的需求,如果您是初学者,建议从Math.sqrt()开始练习;高级开发者可探索算法优化。
引用说明:本文内容基于Oracle Java官方文档、IEEE 754标准及经典算法教材(如《算法导论》),具体参考来源包括:
- Oracle Java Math类文档:https://docs.oracle.com/javase/8/docs/api/java/lang/Math.html
- Newton-Raphson方法详解:Numerical Recipes in C (Cambridge University Press)
- 浮点数处理标准:IEEE 754-2019 Specification