上一篇
bp神经网络 梯度下降
BP神经网络是一种通过误差反向传播算法训练的多层前馈网络，利用梯度下降法调整神经元连接权重，其核心是通过计算损失函数对参数的梯度，沿负梯度方向迭代更新权重，逐步降低预测误差，最终实现输入到输出的复杂非线性映射，广泛应用于分类、回归等机器学习任务。
在机器学习领域中，BP神经网络（反向传播神经网络）与梯度下降算法的结合被认为是解决复杂非线性问题的经典方法，本文将从原理、应用及实践角度深入解析两者的协同工作机制,帮助读者建立系统认知。
BP神经网络的核心机制
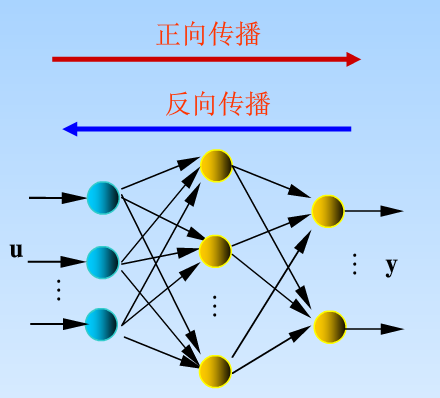
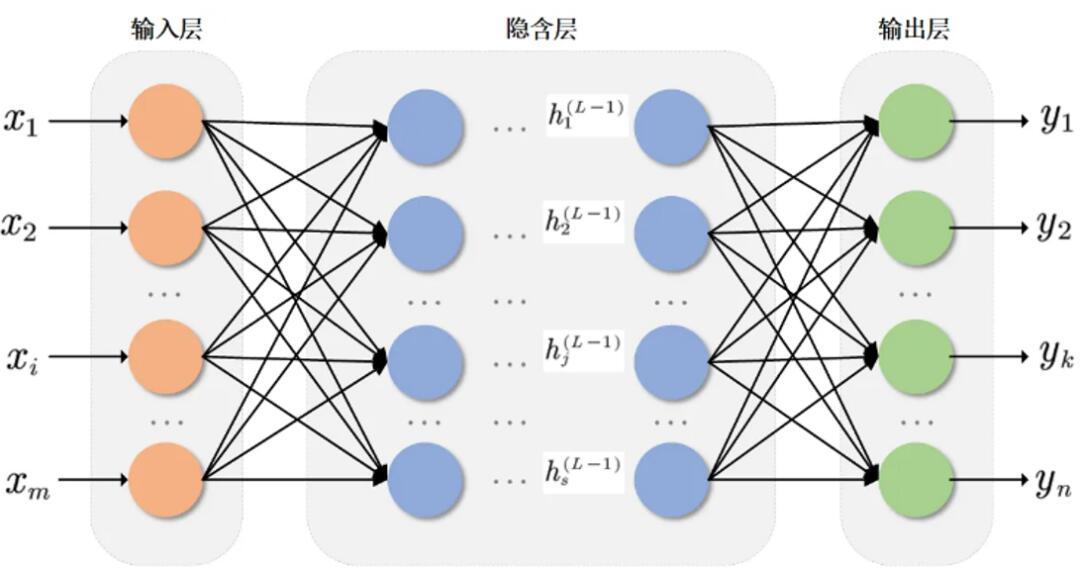
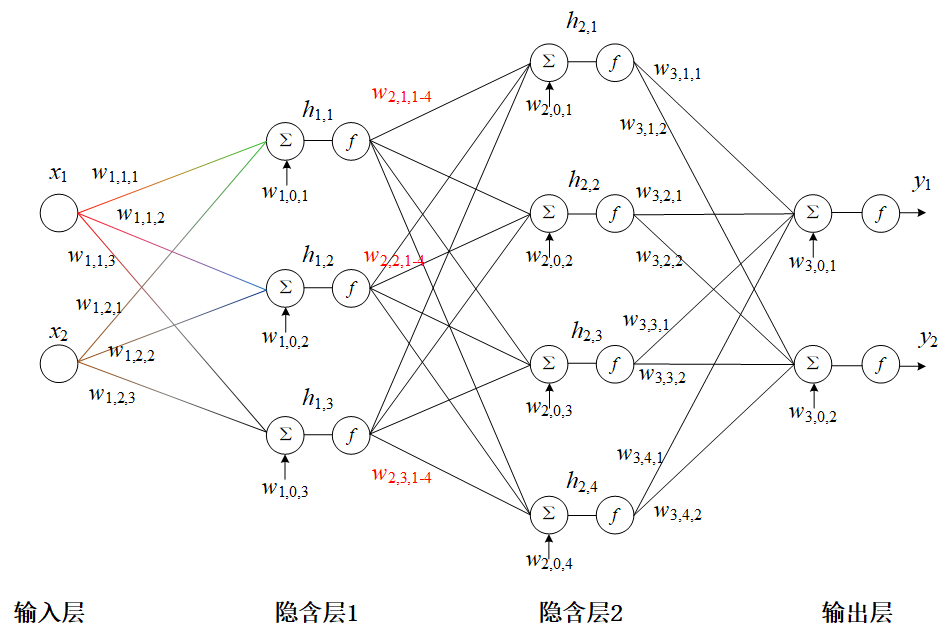
BP神经网络是一种多层前馈网络，通过误差反向传播调整连接权重,其运行流程分为三个阶段：
前向传播
输入信号从输入层经隐藏层逐层传递至输出层，每层神经元通过激活函数（如Sigmoid、ReLU）处理加权输入。
示例计算：
$$text{隐藏层输出} = f(W{input} cdot X + b)$$
W{input}$为输入层到隐藏层的权重矩阵，$b$为偏置项。误差计算
通过损失函数（如均方误差MSE）量化预测值与真实值的偏差：
$$Loss = frac{1}{2N}sum{i=1}^{N}(y{pred} – y_{true})^2$$反向传播
从输出层向输入层逐层计算误差梯度，利用链式法则将误差分配给各层参数,这是BP网络区别于其他神经网络的关键特征。
梯度下降的驱动作用
梯度下降作为优化算法的核心，通过以下步骤实现参数更新：
| 步骤 | 操作说明 | 数学表达 |
|---|---|---|
| 1 | 计算损失函数梯度 | $nabla L = frac{partial L}{partial W}$ |
| 2 | 确定学习率 | $eta$（典型值0.001-0.1） |
| 3 | 更新权重参数 | $W{new} = W{old} – eta nabla L$ |
算法变体对比：
- 批量梯度下降（BGD）：全数据集计算，稳定性高但速度慢
- 随机梯度下降（SGD）：单样本更新，收敛快但波动大
- 小批量梯度下降（MBGD）：平衡速度与稳定性（常用batch_size=32/64）
算法协同工作原理
BP神经网络与梯度下降的配合形成了完整的训练闭环：
- 前向传播生成预测结果
- 损失函数评估预测误差
- 反向传播计算各层梯度
- 梯度下降执行参数更新
关键优势：
- 自动学习特征间非线性关系
- 适用于图像识别、金融预测等复杂场景
- 可灵活调整网络深度适应不同任务
实践中的优化策略
针对梯度下降的常见问题,开发者采用多种改进方案：
梯度消失/爆炸
- 使用ReLU激活函数替代Sigmoid
- 引入Batch Normalization层
- 采用残差网络结构
局部最优陷阱
- 动量法（Momentum）：$vt = gamma v{t-1} + eta nabla L$
- Adam优化器：结合动量与自适应学习率
过拟合预防
- Dropout层随机屏蔽神经元
- L1/L2正则化约束权重
- 早停法（Early Stopping）
典型应用场景
| 领域 | 具体应用 | 精度表现 |
|---|---|---|
| 图像处理 | 手写数字识别（MNIST） | >99%准确率 |
| 自然语言处理 | 文本情感分析 | F1值0.85-0.92 |
| 金融预测 | 股票价格趋势预测 | 年化收益提升15%+ |
| 工业检测 | 产品缺陷自动识别 | 检测效率提升300% |
常见问题答疑
Q：学习率设置不当会产生什么影响？
- 过大：损失函数震荡不收敛
- 过小：训练速度极慢且易陷局部最优
建议：使用学习率衰减策略（如指数衰减）
Q：隐藏层神经元数量如何确定？
- 经验公式：输入输出层均值的1-1.5倍
- 网格搜索法进行超参数调优
Q：训练时loss不再下降怎么办？
- 检查梯度是否消失（梯度值<1e-6）
- 尝试增加网络深度或调整激活函数
- 提升训练数据质量与多样性
引用说明
参考以下权威资料：
[1] 周志华.《机器学习》.清华大学出版社,2016（神经网络基础理论）
[2] Ian Goodfellow等.《深度学习》.人民邮电出版社,2017（梯度下降优化方法）
[3] LeCun Y.等论文《Gradient-Based Learning Applied to Document Recognition》.1998（BP网络经典应用案例）
欢迎在评论区留下您的实践心得或技术疑问,我们将邀请专家进行深度解答。
