如何用单片机实现跳一跳物理引擎？

想象一下,你指尖操控的小人在屏幕上精准地从一个平台跳到另一个平台，距离、落点、甚至微妙的抛物线轨迹都恰到好处——这背后离不开精妙的物理模拟，而当我们谈论在资源受限的单片机上实现类似“跳一跳”游戏的核心物理引擎时，这本身就是一场对硬件极限和软件智慧的挑战，本文将深入解析单片机如何驾驭这看似简单的“一跳”所蕴含的复杂物理世界。

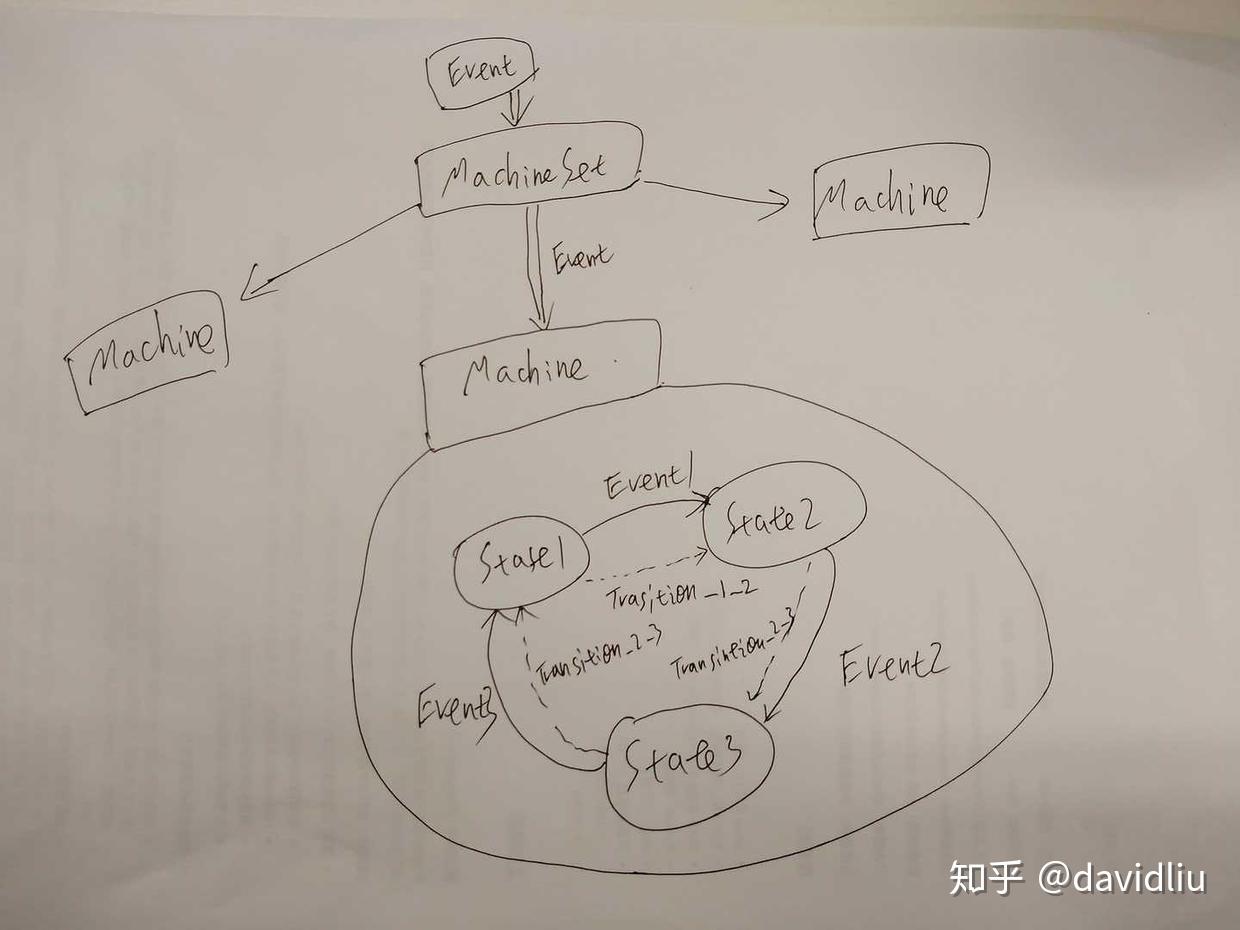
“跳一跳”的核心物理：不只是简单的距离

在表象之下,“跳一跳”游戏的核心物理模型主要围绕以下几个关键点：

1. 蓄力与初速度： 玩家按压屏幕的时间长短决定了跳跃的“力度”，在物理上，这通常转化为跳跃的初始速度 (v0)，按压时间 (t_press) 与 v0 的关系可以是线性的，也可以是非线性的（例如二次方），以模拟蓄力感。

   • v0 = k * t_press (线性模型)
   • v0 = k * (t_press)^2 (非线性模型，更接近真实蓄力) k 是比例系数。

2. 抛物线轨迹： 一旦小人离开平台，它将在重力的作用下做抛体运动，其运动轨迹是一条标准的抛物线，要精确模拟，单片机需要实时计算小人在每一时刻的位置 (x, y)：

   • 水平方向 (x轴)： 匀速直线运动。 x = x0 + vx0 * t (x0 是起跳点，vx0 是水平初速度分量，t 是起跳后时间)
   • 垂直方向 (y轴)： 匀加速直线运动（加速度向下，为重力加速度 g）。 y = y0 + vy0 * t - (1/2) * g * t^2 (y0 是起跳高度，vy0 是垂直初速度分量)
   • 关键点： 水平初速度 vx0 和垂直初速度 vy0 由总的初始速度 v0 和跳跃角度 (θ) 决定：
     • vx0 = v0 * cos(θ)
     • vy0 = v0 * sin(θ)
   • 在经典的“跳一跳”中，跳跃方向通常是固定的（例如水平向右），因此角度 θ 是常量（可能是 45° 或根据平台位置动态微调），简化了计算。v0 的大小则由按压时间决定。

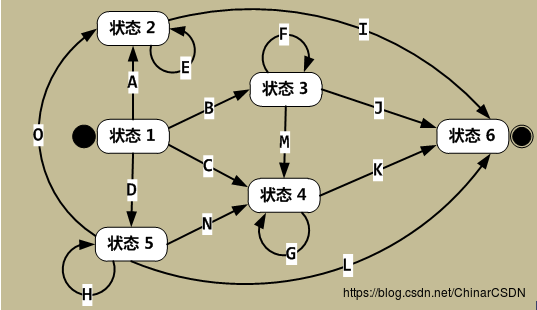
3. 碰撞检测： 这是游戏逻辑成败的关键，当小人沿着抛物线下落时，单片机需要持续判断其边界（通常简化为一个点或一个小矩形/圆形）是否与目标平台的边界发生碰撞。

   

   • 检测时机： 通常在小人达到轨迹最高点之后的下落阶段进行密集检测。
   • 检测方法：
     • 边界框检测 (AABB)： 将小人和平台视为轴对齐的矩形，判断小人的矩形是否与平台矩形相交，计算相对简单，适合单片机。
     • 点与矩形检测： 将小人简化为一个点（例如其底部中心点），判断该点是否落在目标平台矩形区域内，这是最常用的简化方法。
   • 精确性要求： 需要精确判断落点是“完美中心”、“边缘安全区”还是“落空”，这决定了得分和游戏是否继续。

4. 物理反馈：

   • 成功着陆： 小人平稳停在平台上，可能伴随轻微震动或粒子效果（在单片机能力范围内）。
   • 边缘着陆： 小人可能晃动或仅部分落在平台上，游戏继续但得分较低。
   • 落空： 小人继续下落，游戏结束。

单片机如何实现这个物理引擎？

在资源（CPU主频、内存、浮点运算能力）有限的单片机上实现上述物理模拟，需要精心设计和优化：

1. 数据采集 (输入)：

   • 通过ADC读取按键按压时间或触摸屏按压时间,得到 t_press。
   • 可能通过加速度计读取设备倾斜角度,动态调整跳跃方向或重力参数（增强版）。

2. 物理计算 (核心处理)：

   • 计算初速度 v0： 根据 t_press 和预设的映射关系（查表法或简单公式计算）得到 v0。
   • 分解速度： 根据固定的或动态的跳跃角度 ，计算 vx0 和 vy0。优化关键： 避免实时计算 sin(θ) 和 cos(θ)！通常做法：
     • 查表法 (LUT)： 预先计算好常用角度（或 v0 方向）对应的 sin/cos 值，存储在ROM中，使用时直接查找，这是单片机最常用的优化手段。
     • 定点数运算： 使用定点数代替浮点数进行所有物理计算（位置、速度、时间），可以极大提高计算速度和减少内存占用，需要仔细处理精度和范围。
     • 简化模型： 如果角度固定（如45°），则 sin(45°) = cos(45°) ≈ 0.707，直接用常数乘以 v0 得到 vx0 和 vy0。
   • 轨迹模拟 (状态更新)：
     • 使用一个定时器中断（例如每 10ms 或 20ms）作为物理更新的时间步长 Δt。
     • 在每个中断服务程序 (ISR) 中：
       • 更新运动时间： t = t + Δt
       • 计算新位置：
         • x = x0 + vx0 * t (水平匀速)
         • y = y0 + vy0 * t - 0.5 * g * t * t (垂直匀加速) 优化关键： g*t*t 可以预先计算好不同 t 下的值存入LUT，或者使用迭代法避免每次计算平方。
     • 将计算出的 (x, y) 坐标转换为屏幕坐标，更新小人的显示位置。

3. 碰撞检测 (逻辑判断)：

   • 在更新小人位置后（尤其是在下落阶段），根据选定的检测方法（点检测或AABB）：
     • 获取目标平台的边界坐标（通常存储在数组中）。
     • 判断小人当前位置（或边界）是否满足碰撞条件（platform_left < x < platform_right 且 y ≈ platform_top）。
     • 根据碰撞点与平台中心的距离判断着陆精度（完美、边缘）。

4. 结果反馈 (输出)：

   • 根据碰撞检测结果,更新游戏状态（成功、边缘、失败）。
   • 控制显示屏刷新,绘制小人新的位置和可能的着陆效果。
   • 可能通过PWM驱动蜂鸣器或马达提供音效或震动反馈。

挑战与优化：单片机的物理之道

在单片机上流畅运行物理引擎面临独特挑战：

• 有限的计算能力： 浮点运算（尤其是乘除、三角函数、平方）在无FPU的单片机上非常慢。解决方案： 优先使用查表法(LUT)、定点数运算、简化物理模型（如固定角度、简化重力计算）、迭代法更新位置（避免重复计算完整公式）。
• 实时性要求： 物理更新和画面刷新需要在严格的时间限制内完成，否则游戏会卡顿。解决方案： 精心设计中断服务程序(ISR)，确保其执行时间短；将耗时计算（如复杂碰撞检测）拆分到主循环中；使用高效的算法和数据结构。
• 内存限制： LUT会占用ROM，存储平台信息、状态变量需要RAM。解决方案： 优化数据结构，使用较小的数据类型（uint8_t, int16_t）；只存储必要的信息；压缩LUT数据（如存储差值）。
• 精度与稳定性： 定点数运算和简化模型会引入误差，长时间运行可能导致累计误差。解决方案： 选择合适的定点数格式（Q格式）；定期重置或校正参考点；在关键点（如着陆判断）使用更高精度计算。

硬件要求：选择合适的单片机

并非所有单片机都适合,需要考虑：

• 足够的主频： 建议48MHz或更高，确保能及时处理物理计算、显示刷新和输入响应。
• 内存 (RAM/ROM)： 足够的RAM存储游戏状态、位置变量、平台数据；足够的ROM存储代码、LUT、图形资源。
• 外设：
  • ADC： 用于读取按键/触摸按压时间。
  • 定时器： 精确控制物理更新和显示刷新率。
  • 显示接口： SPI/I2C驱动OLED或LCD屏幕。
  • GPIO： 连接按键、LED、蜂鸣器等。
  • (可选) 加速度计接口： SPI/I2C，用于增强交互。
• (推荐) 硬件FPU： 如果使用带硬件浮点单元(FPU)的单片机（如某些ARM Cortex-M4F/M7），可以显著简化浮点运算，提高精度和速度，降低优化难度。

在单片机上实现“跳一跳”的物理引擎，是将经典力学原理（抛体运动、碰撞）在资源受限环境下的精巧实践，它要求开发者深刻理解物理模型，并熟练掌握针对单片机的优化技术：查表法、定点数运算、状态机设计、高效中断处理，这不仅仅是让一个小像素点跳跃起来，更是对单片机实时计算能力、资源管理能力和开发者工程智慧的考验，成功的实现，能让玩家在简单的操作中感受到流畅、精准且符合直觉的物理反馈，这正是单片机在互动娱乐领域展现独特魅力的地方。

引用说明：

• 本文涉及的物理原理（抛体运动公式）源自经典力学，是物理学的基础知识，可参考标准物理学教材如《Halliday and Resnick’s Fundamentals of Physics》。
• 单片机优化技术（查表法、定点数运算、状态机）是嵌入式系统开发的通用实践，可参考权威嵌入式编程书籍如《Making Embedded Systems》 by Elecia White 或 《Programming Embedded Systems》 by Michael Barr。
• 关于特定单片机架构（如ARM Cortex-M）的定时器、ADC、FPU使用细节，请参考相应芯片厂商（如STMicroelectronics, NXP, Microchip）提供的官方参考手册和数据手册，这些文档是硬件操作的最高权威来源。
• 游戏物理引擎设计思想可参考经典著作如《Game Physics Engine Development》 by Ian Millington (尽管该书面向高性能平台，其基本原理同样适用)。