如何高效存储和处理图中的父节点与子节点?
- 行业动态
- 2025-04-29
- 2
存储图中的父节点和子节点通常通过数据结构维护层级关系,如树或图结构中每个节点存储指向父节点的引用及子节点列表,常见实现方式包括父指针与子节点数组结合,或使用邻接表记录双向关联,确保快速查询与遍历操作的高效性。
在计算机科学和数据库设计中,父子节点的存储是处理树形结构或层级关系数据的核心问题,无论是电商平台的分类目录、组织架构的上下级关系,还是社交网络的关注体系,都需要高效且可扩展的存储方案,本文将从数据结构、数据库设计、实际应用等多个维度展开分析。
父子节点关系的核心挑战
父子节点的存储需要解决以下关键问题:
- 快速查询父子关系:例如查找某个节点的直接子节点或所有祖先节点。
- 层级遍历效率:例如统计某分类下的所有商品,或计算组织架构的深度。
- 动态更新的灵活性:例如移动子树、插入新节点时避免大规模数据修改。
- 存储空间优化:避免因冗余数据占用过多资源。
常见存储方案与实现
方案1:邻接表(Adjacency List)
原理:每个节点存储其直接父节点的ID。
数据结构示例(SQL表):
CREATE TABLE nodes (
id INT PRIMARY KEY,
name VARCHAR(50),
parent_id INT,
FOREIGN KEY (parent_id) REFERENCES nodes(id)
);优点:
- 结构简单,插入、删除节点速度快(时间复杂度O(1))。
- 适合层级较浅或更新频繁的场景(如评论区盖楼)。
缺点:
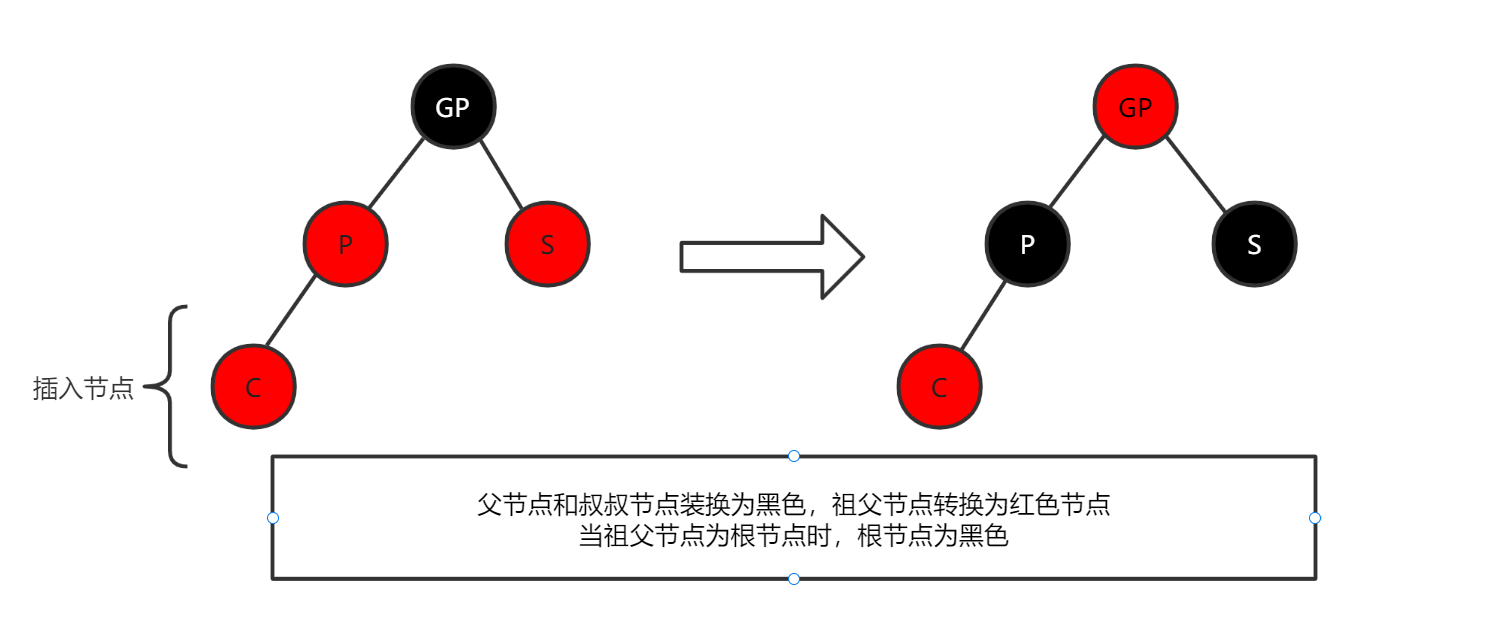
- 查询所有子孙节点需要递归操作,性能随层级深度下降(时间复杂度O(n))。
- 难以直接统计子树规模或深度。
方案2:闭包表(Closure Table)
原理:通过额外的关系表记录所有祖先-后代路径。
数据结构示例(SQL表):
CREATE TABLE node_closure (
ancestor_id INT,
descendant_id INT,
depth INT,
PRIMARY KEY (ancestor_id, descendant_id),
FOREIGN KEY (ancestor_id) REFERENCES nodes(id),
FOREIGN KEY (descendant_id) REFERENCES nodes(id)
);优点:
- 支持快速查询任意层级的父子关系(如直接查询depth=1获取子节点)。
- 可一次性获取所有祖先或后代,适合复杂层级分析。
缺点:
- 存储空间随节点数平方级增长,需定期维护。
- 插入新节点时需更新多条闭包记录。
方案3:物化路径(Materialized Path)
原理:为每个节点存储从根节点到自身的完整路径。
数据结构示例(MongoDB文档):
{
"_id": 101,
"name": "智能手机",
"path": "1.5.101" // 根节点为1(消费电子),父节点为5(手机)
}优点:
- 通过路径字符串匹配(如
LIKE '1.5.%')快速查询子树。 - 天然支持排序和层级展示。
缺点:
- 路径长度受限,节点迁移需更新所有后代路径。
- 频繁的字符串操作可能影响性能。
方案4:嵌套集合(Nested Sets)
原理:通过左值(left)和右值(right)标记节点的遍历范围。
数据结构示例(SQL表):
CREATE TABLE nested_nodes (
id INT PRIMARY KEY,
name VARCHAR(50),
lft INT,
rgt INT
);优点:
- 查询子树或祖先节点无需递归,仅需范围判断(时间复杂度O(1))。
- 适合静态或低频更新的层级(如商品分类)。
缺点:
- 插入或移动节点需重新计算左右值,维护成本高。
- 对并发写入不友好。
方案对比与选型建议
| 方案 | 查询效率 | 写入效率 | 空间占用 | 适用场景 |
|---|---|---|---|---|
| 邻接表 | 低 | 高 | 低 | 简单层级、频繁更新 |
| 闭包表 | 高 | 中 | 高 | 复杂查询、分析统计 |
| 物化路径 | 中 | 中 | 低 | 固定层级、路径依赖 |
| 嵌套集合 | 高 | 低 | 中 | 静态数据、只读为主 |
实际应用中的优化技巧
- 混合模型:例如结合邻接表与闭包表,平衡查询和写入效率。
- 异步更新:对闭包表或嵌套集合的维护操作放入后台任务。
- 索引优化:对路径字段(如物化路径)建立前缀索引,加速LIKE查询。
- 缓存机制:将高频访问的层级关系缓存在Redis等内存数据库中。
- 事务支持:在移动子树时,通过数据库事务保证数据一致性。
代码示例:邻接表的递归查询
class Node:
def __init__(self, id, parent_id=None):
self.id = id
self.parent_id = parent_id
def find_ancestors(node_id, nodes):
ancestors = []
current = nodes.get(node_id)
while current and current.parent_id:
parent = nodes.get(current.parent_id)
ancestors.append(parent.id)
current = parent
return ancestors
# 示例数据
nodes = {
101: Node(101, 5),
5: Node(5, 1),
1: Node(1)
}
print(find_ancestors(101, nodes)) # 输出 [5, 1]父子节点的存储方案需根据数据规模、查询模式、更新频率综合权衡,对于中小型项目,邻接表凭借简单易用仍是首选;而面对复杂的层级分析需求(如权限继承、组织架构统计),闭包表或物化路径更能体现优势,随着图数据库(如Neo4j)的普及,基于属性图的存储方式可能成为新的趋势。
引用说明
本文涉及的数据库设计方法参考自《SQL反模式》(Bill Karwin著)及MySQL官方文档;算法实现部分基于《算法导论》(Thomas H. Cormen等)中的树遍历理论。