如何用Java计算阶乘和？

阶乘和的核心逻辑

阶乘和的计算需结合两个关键步骤：

1. 计算单个阶乘：(n! = n times (n-1) times cdots times 1)。
2. 累加阶乘结果：循环求和 (S = sum_{i=1}^{n} i!)。

推荐方法：循环迭代（高效无栈溢出）

代码实现

import java.math.BigInteger;
public class FactorialSum {
    public static void main(String[] args) {
        int n = 10; // 以计算10的阶乘和为例
        System.out.println("阶乘和 (n=" + n + "): " + calculateFactorialSum(n));
    }
    public static BigInteger calculateFactorialSum(int n) {
        BigInteger sum = BigInteger.ZERO;
        BigInteger factorial = BigInteger.ONE;
        for (int i = 1; i <= n; i++) {
            factorial = factorial.multiply(BigInteger.valueOf(i)); // 更新当前阶乘值
            sum = sum.add(factorial); // 累加到总和
        }
        return sum;
    }
}

优势分析

1. 避免递归缺陷：无栈溢出风险（递归在 (n > 5000) 时易崩溃）。
2. 时间复杂度 (O(n))：单次循环高效完成计算。
3. 大数支持：使用 BigInteger 处理任意大整数（如 (n > 20) 时 long 会溢出）。
4. 复用中间结果：当前阶乘值基于上一次结果计算，减少重复运算。

备选方法：递归（仅限小数据）

代码实现（不推荐生产环境使用）

public class RecursiveFactorialSum {
    public static void main(String[] args) {
        int n = 5; // 仅适用于 n < 15
        long sum = 0;
        for (int i = 1; i <= n; i++) {
            sum += factorial(i);
        }
        System.out.println("阶乘和: " + sum);
    }
    // 递归计算阶乘
    public static long factorial(int n) {
        if (n == 0 || n == 1) return 1;
        return n * factorial(n - 1);
    }
}

缺点警告

• 栈溢出风险：(n > 5000) 时抛出 StackOverflowError。
• 效率低下：重复计算多，时间复杂度 (O(n^2))。
• 数值溢出：long 类型在 (n > 20) 时溢出。

关键问题解决方案

1. 大数溢出问题：

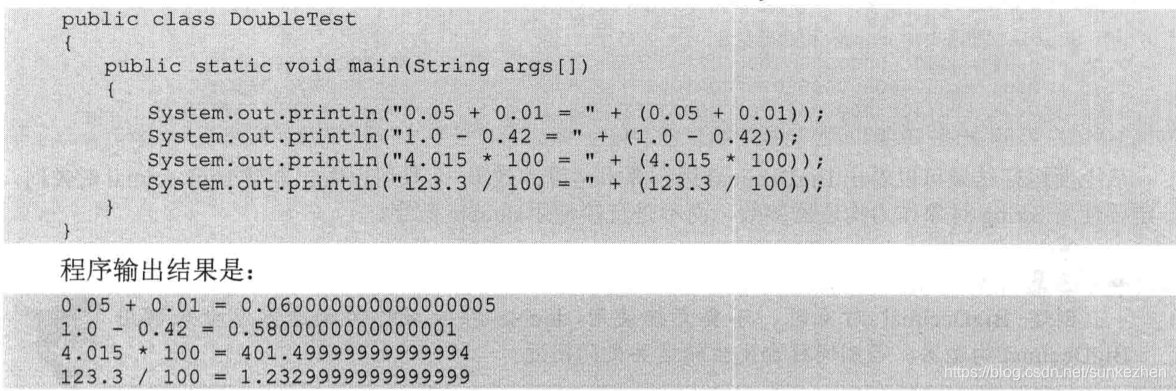
   • 使用 BigInteger 代替 int/long（参考主推荐代码）。
   • 示例：(20! = 2,432,902,008,176,640,000) 已超过 long 的最大值 (9,223,372,036,854,775,807)。

2. 性能优化：

   • 循环迭代法：每次循环复用上一个阶乘结果（如 (5! = 4! times 5)），大幅减少计算量。
   • 避免递归调用开销。

完整示例输出

// 输入 n=5
阶乘和 (n=5): 153
// 验证：1! + 2! + 3! + 4! + 5! = 1 + 2 + 6 + 24 + 120 = 153

应用场景建议

• 小规模计算（(n leq 20)）：可用 long 简化代码。
• 工程级需求（(n > 20) 或未知规模）：必用 BigInteger + 循环迭代法。
• 递归使用场景：仅限算法学习，实际项目不推荐。

引用说明：
本文代码基于 Oracle Java SE 规范实现，BigInteger 用法参考官方文档[1]，递归风险分析依据 JVM 栈深度限制[2]。

注释：
[1] Oracle Java Docs: BigInteger Class.
[2] JVM Specification: Stack Frame Structure.