从线性回归到深度学习

从线性回归到深度学习，是机器学习领域不断发展和演进的过程。

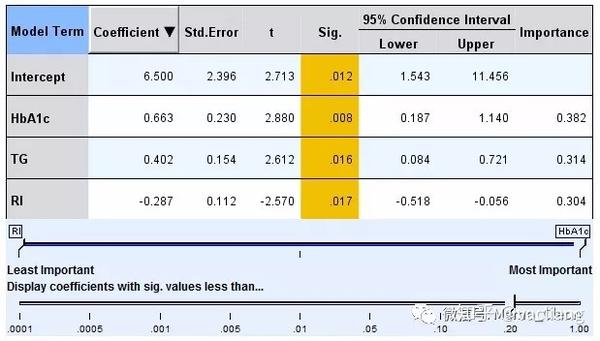
线性回归

基本概念：线性回归是一种基础的监督学习算法，主要用于处理回归问题，也就是预测连续型数值变量，它基于一个自变量（特征）和一个因变量（目标）之间的线性关系建立数学模型，其核心思想是通过找到一条最佳拟合直线，使得所有数据点到这条直线的距离之和最小化，通常使用最小二乘法来确定这个最优解。

特点与局限性：优点是简单易懂、计算量小、易于实现，对于一些简单的线性关系问题能够快速得到结果，它的局限性也很明显，它假设变量之间是线性关系，但现实世界中很多问题并非如此；它对异常值敏感，少数异常数据可能会对模型产生较大影响；而且它只能处理一个因变量的情况，无法直接处理多变量问题。

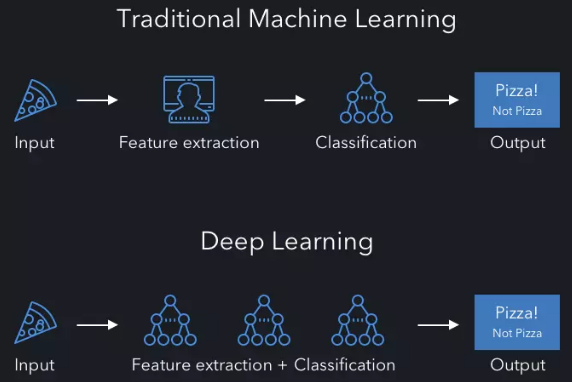
深度学习

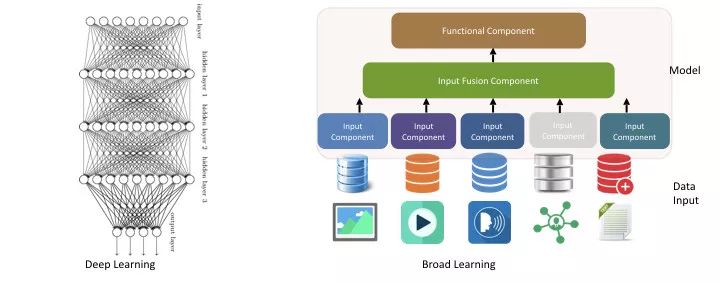
基本概念：深度学习是机器学习的一个分支，它以人工神经网络为基础，通过构建多层神经网络来自动地从大量数据中学习复杂的模式和特征表示，这些神经网络由多个神经元层组成，每层包含多个神经元，每个神经元接收上一层神经元的输出作为输入，并通过激活函数进行非线性变换后输出给下一层。

特点与优势：可以自动提取数据的特征，无需手动设计特征工程，能够处理复杂的非线性关系；具有强大的泛化能力，在训练数据充足的情况下，能够很好地推广到未见过的数据上；可以通过增加网络层数和神经元数量来提高模型的复杂度和容量，从而更好地拟合数据。

典型算法：包括卷积神经网络（CNN）、循环神经网络（RNN）及其变体长短期记忆网络（LSTM）、生成对抗网络（GAN）等，CNN 主要用于处理图像相关的任务，如图像识别、目标检测等；RNN 和 LSTM 适用于处理序列数据，如自然语言处理中的文本生成、语音识别等；GAN 则常用于生成新的数据样本，如生成逼真的图像、音频等。

从线性回归到深度学习的发展脉络

数据处理能力的提升：线性回归只能处理简单的线性关系，而深度学习能够处理复杂的非线性关系，这是由于深度学习中的多层神经网络结构和非线性激活函数的作用，在图像识别中，线性回归无法很好地处理图像中的边缘、纹理等复杂特征，而深度学习可以通过多层卷积层自动提取这些特征，从而实现更准确的识别。

模型复杂度的增加：线性回归模型相对简单，只有一个线性方程，而深度学习模型通常具有大量的参数和多层结构，可以更好地拟合数据，一个简单的线性回归模型可能只有几个参数，而一个深度神经网络模型可能有数百万甚至数十亿个参数，这使得深度学习模型能够捕捉到数据中的更多细节和复杂模式。

应用场景的拓展：线性回归在一些简单的预测问题上有一定的应用，但深度学习的应用场景更加广泛，除了常见的图像识别、语音识别、自然语言处理等领域，深度学习还在医疗、金融、交通等众多领域得到了广泛应用，在医疗领域，深度学习可以用于疾病诊断、医学图像分析等；在金融领域，可以用于风险评估、股票价格预测等。

实际应用案例对比

图像识别：线性回归在图像识别中效果不佳，因为图像的特征是高度非线性的，而深度学习中的 CNN 可以自动学习图像的特征，如边缘、纹理、形状等，从而实现高精度的图像识别，在手写数字识别中，CNN 可以轻松地识别出不同手写风格的数字，准确率远高于线性回归。

自然语言处理：线性回归难以处理自然语言中的复杂语义和语法关系，而深度学习中的 RNN 和 LSTM 可以处理序列数据，如文本中的单词顺序、句子结构等，从而实现机器翻译、文本生成、情感分析等任务，在机器翻译中，RNN 可以将一种语言的句子转换为另一种语言的句子，并且能够较好地保留原文的语义和语法信息。

从线性回归到深度学习是机器学习领域不断发展和进步的过程，线性回归作为一种基础的算法，为理解机器学习的基本概念提供了帮助，但在处理复杂问题时存在局限性，而深度学习凭借其强大的数据处理能力、复杂的模型结构和广泛的应用场景，成为了当前机器学习领域的研究热点和应用主流，随着技术的不断发展，深度学习将继续发挥重要作用，并不断推动人工智能领域的发展。

相关问答FAQs

1、线性回归和深度学习都可以用于预测，它们的主要区别在哪里？

线性回归是一种简单的回归分析方法，它假设自变量和因变量之间存在线性关系，通过最小化误差平方和来求解模型参数，它适用于数据量较小、变量关系较为简单且近似线性的场景，而深度学习是一种基于多层神经网络的机器学习方法，它可以自动从大量数据中学习复杂的非线性关系和特征表示，适用于处理复杂的、非线性的、高维的数据，如图像、语音、文本等。

2、深度学习一定比线性回归好吗？

不一定，虽然深度学习在处理复杂数据和任务方面具有很强的优势，但它也有一些缺点，如需要大量的数据和计算资源、训练时间较长、模型解释性较差等，对于一些简单的问题或者数据量较小的情况，线性回归可能是一种更合适的选择，选择哪种方法取决于具体的问题、数据特点以及应用需求。