当前位置：首页 > 行业动态 > 正文

bp 神经网络推导

admin
行业动态
2025-04-10
1

BP神经网络通过反向传播算法调整权重参数，利用梯度下降法最小化预测误差，其推导核心为链式法则求导，将输出层误差逐层反向传播至各隐藏层，计算梯度并更新权重，该过程包含前向计算损失和反向迭代优化两个阶段，适用于监督学习任务中的模型训练。

神经网络作为机器学习领域的重要模型，其核心算法反向传播（Backpropagation，BP）通过误差的逆向传播实现参数优化，本文以严谨的数学推导为基础，通过四步解析BP算法原理,帮助读者建立系统认知。

神经网络基本原理

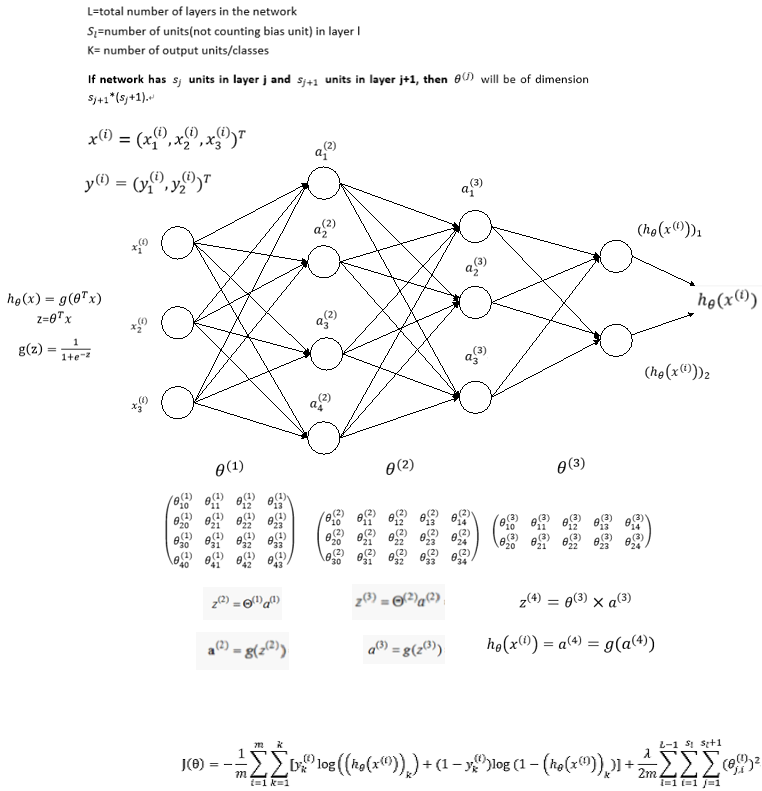
三层前馈神经网络是BP算法的典型结构,包含：

输入层：接收原始数据（特征向量）
隐含层：通过激活函数处理线性组合
输出层：生成最终预测结果

设网络包含$L$层,参数表示为：

$w_{ij}^{(l)}$：第$l$层第$j$神经元到第$l+1$层第$i$神经元的权重
$b_i^{(l)}$：第$l+1$层第$i$神经元的偏置
$z_i^{(l)}$：第$l$层第$i$神经元的加权输入
$a_i^{(l)}$：第$l$层第$i$神经元的激活值

数学推导过程

前向传播

对于第$l$层第$i$神经元：
$$
begin{aligned}
zi^{(l)} &= sum{j} w_{ij}^{(l-1)}a_j^{(l-1)} + b_i^{(l-1)}
a_i^{(l)} &= sigma(z_i^{(l)})
end{aligned}
$$
sigma(cdot)$为激活函数（如Sigmoid、ReLU）

bp 神经网络推导第1张

损失函数

以均方误差（MSE）为例：
$$
E = frac{1}{2}sum_{k=1}^{K}(y_k – a_k^{(L)})^2
$$
$K$为输出层神经元数量，$y_k$为真实值

反向传播

关键推导：利用链式法则计算梯度

(1) 输出层梯度
对输出层权重$w{ij}^{(L-1)}$：
$$
frac{partial E}{partial w{ij}^{(L-1)}} = underbrace{(a_j^{(L)} – yj)}{delta_j^{(L)}} cdot sigma'(z_j^{(L)}) cdot a_i^{(L-1)}
$$
delta_j^{(L)} = (a_j^{(L)} – y_j)sigma'(z_j^{(L)})$称为误差项

(2) 隐含层梯度
对第$l$层权重$w{ij}^{(l)}$：
$$
frac{partial E}{partial w{ij}^{(l)}} = delta_i^{(l+1)} cdot a_j^{(l)}
$$
误差反向传播公式：
$$
deltaj^{(l)} = left( sum{k} deltak^{(l+1)}w{kj}^{(l)} right) sigma'(z_j^{(l)})
$$