当前位置：首页 > 行业动态 > 正文

bp 神经网络程序

在人工智能领域,BP神经网络作为监督学习的核心算法之一，凭借其强大的非线性映射能力和通用性，被广泛应用于图像识别、金融预测、工业控制等场景，本文将通过可复现的代码示例和理论剖析，为开发者提供一份从零构建BP神经网络的实用指南。

BP神经网络的核心原理

BP神经网络(误差反向传播网络)由输入层、隐藏层和输出层构成，通过以下机制实现模型训练：

  1. 前向传播：输入数据逐层加权计算，经激活函数处理产生预测值
    $yk = fleft(sum w{jk} cdot h_j + b_kright)$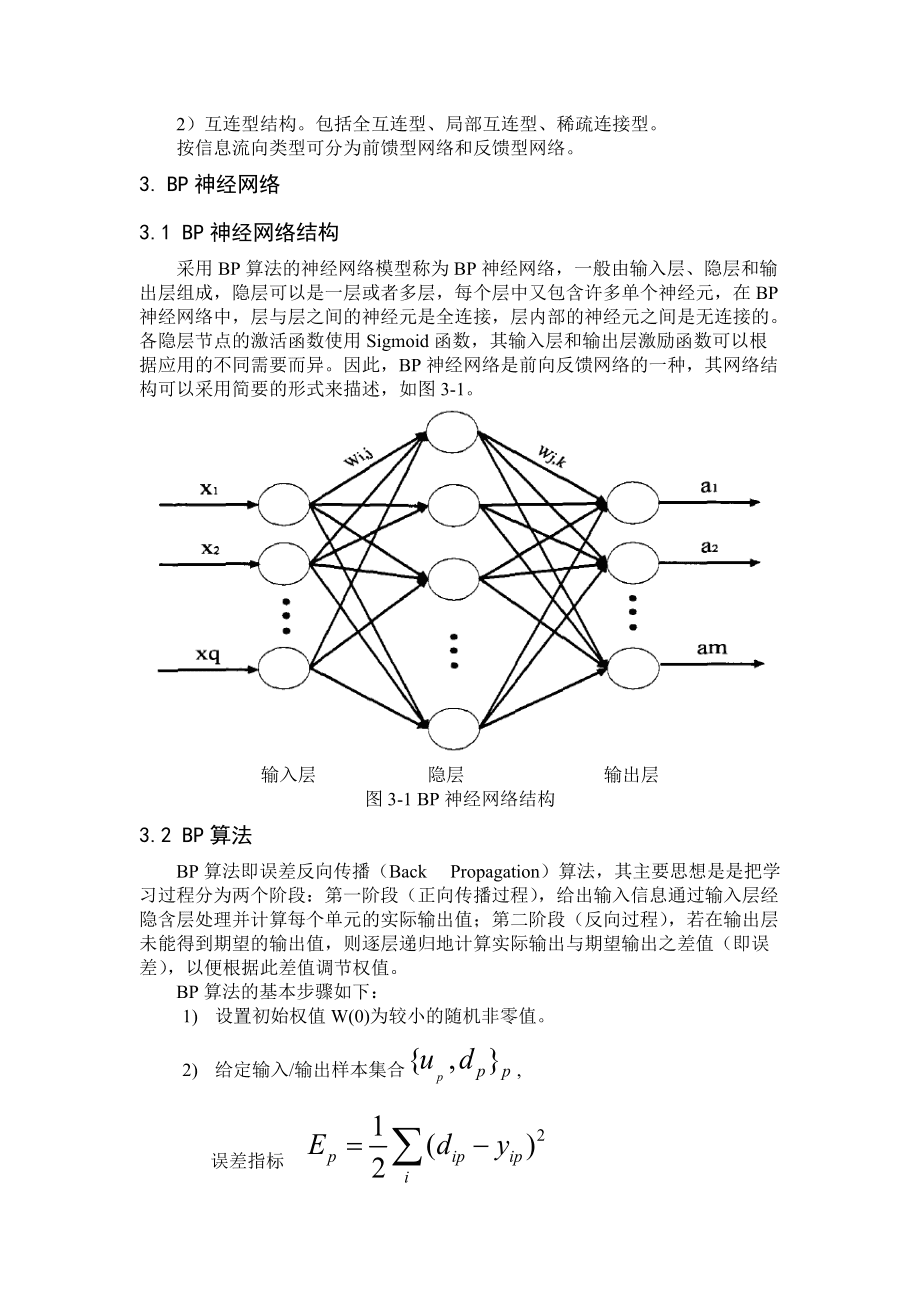

    bp 神经网络程序 第1张

  2. 误差计算：采用均方误差函数度量预测偏差
    $E = frac{1}{2}sum (t_k – y_k)^2$

  3. 反向传播：基于梯度下降法逐层调整参数
    $Delta w{jk} = -eta frac{partial E}{partial w{jk}}$

Python实现步骤（附完整代码）

以下示例使用NumPy实现三层网络对异或(XOR)问题的分类：

import numpy as np
# 激活函数与导数
def sigmoid(x):
    return 1/(1 + np.exp(-x))
def sigmoid_derivative(x):
    return x*(1 - x)
# 网络参数
input_size = 2
hidden_size = 4
output_size = 1
learning_rate = 0.1
epochs = 10000
# 初始化权重
W1 = np.random.randn(input_size, hidden_size)
W2 = np.random.randn(hidden_size, output_size)
# 训练数据
X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[1],[1],[0]])
# 训练过程
for epoch in range(epochs):
    # 前向传播
    hidden_input = np.dot(X, W1)
    hidden_output = sigmoid(hidden_input)
    final_input = np.dot(hidden_output, W2)
    final_output = sigmoid(final_input)
    # 误差计算
    error = y - final_output
    # 反向传播
    d_output = error * sigmoid_derivative(final_output)
    error_hidden = d_output.dot(W2.T)
    d_hidden = error_hidden * sigmoid_derivative(hidden_output)
    # 权重更新
    W2 += hidden_output.T.dot(d_output) * learning_rate
    W1 += X.T.dot(d_hidden) * learning_rate
# 输出训练结果
print("预测值:n", np.round(final_output,3))

关键实现要点解析

  1. 数据预处理

    • 对特征数据进行标准化处理（如Min-Max Scaling）
    • 分类任务建议对标签进行One-Hot编码

  2. 网络结构设计
    | 参数类型 | 推荐设置 |
    |—————-|———————–|
    | 隐藏层神经元数 | 输入特征数的2/3到2倍 |
    | 激活函数 | 隐藏层ReLU，输出层Sigmoid |
    | 权重初始化 | He初始化或Xavier初始化 |

  3. 性能优化技巧

    • 采用动量优化器(Momentum)加速收敛
    • 添加L2正则化项防止过拟合
    • 实现批量梯度下降提升训练效率

典型问题解决方案

  • 梯度消失：使用ReLU及其变体代替Sigmoid函数
  • 局部极小值：引入随机梯度下降(SGD)的噪声机制
  • 过拟合：增加Dropout层，验证集精度监控

工业级应用扩展

  1. 使用TensorFlow/PyTorch框架实现GPU加速
  2. 集成Keras的EarlyStopping回调功能
  3. 通过MLflow进行实验追踪和模型管理
# 使用Keras的高级API实现
from keras.models import Sequential
from keras.layers import Dense
model = Sequential([
    Dense(4, activation='relu', input_dim=2),
    Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam', 
              loss='binary_crossentropy',
              metrics=['accuracy'])
model.fit(X, y, epochs=1000, verbose=0)

参考文献

  1. Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors[J]. Nature, 1986 (权威理论基础)
  2. Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016 (优化方法参考)
  3. TensorFlow官方文档 https://www.tensorflow.org/ (工程实践指南)
  4. Scikit-learn特征处理指南 https://scikit-learn.org/stable/modules/preprocessing.html (数据预处理规范)
0

相关文章