上一篇
bp神经网络拟合函数大全
- 行业动态
- 2025-04-10
- 5
在机器学习领域中,BP神经网络(误差反向传播神经网络)因其强大的非线性拟合能力,成为解决复杂函数逼近问题的核心工具,本文系统梳理BP神经网络在函数拟合中的典型应用场景、常见函数类型及优化技巧,结合权威文献与工程实践,为读者提供可直接落地的知识框架。
BP神经网络为何擅长函数拟合?
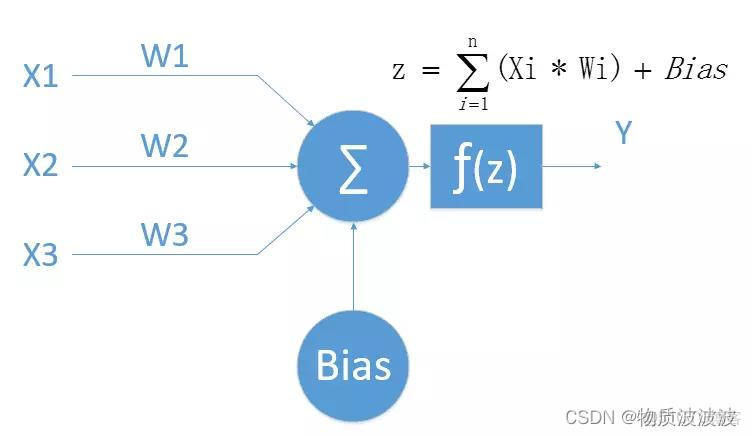
BP神经网络通过多层感知器结构(输入层、隐藏层、输出层)与反向传播算法,能够以任意精度逼近连续非线性函数,其核心优势在于:
- 非线性映射:激活函数(如Sigmoid、ReLU)赋予网络非线性表达能力。
- 自适应学习:梯度下降算法自动调整权重参数,最小化预测误差。
- 泛化能力:通过正则化与交叉验证避免过拟合,适应未知数据。
典型函数拟合场景与实现方法
以下为BP神经网络可高效拟合的6类函数及实现要点:
多项式函数
- 示例:$y = a_0 + a_1x + a_2x^2 + … + a_nx^n$
- 网络设计:输入层1节点(x值),隐藏层节点数≥多项式阶数,输出层1节点(y值)。
- 关键技巧:数据需归一化防止梯度爆炸。
非线性分段函数
- 示例:阶跃函数、符号函数、ReLU函数。
- 网络设计:需增加隐藏层数(通常2~3层),使用ReLU激活函数提升分段拟合效果。
周期函数(正弦/余弦)
- 示例:$y = sin(x) + cos(2x)$
- 网络设计:输入层扩展为多维度(如$x$, $sin(x)$, $cos(x)$),隐藏层使用Tanh激活函数匹配输出范围[-1,1]。
高维曲面函数
- 示例:$z = x^2 + y^2 + xy$
- 网络设计:输入层节点数=自变量维度(如x和y),隐藏层宽度需随维度增加而扩展。
隐函数方程
- 示例:$F(x,y)=0$(如椭圆方程 $frac{x^2}{a^2} + frac{y^2}{b^2} =1$)
- 实现方法:将方程转化为误差函数,通过监督学习逼近解空间。
动态系统函数
- 示例:微分方程 $frac{dy}{dt} = f(y,t)$
- 网络设计:引入时间序列输入,采用LSTM或RNN结构捕捉时序依赖。
提升拟合效果的5大优化技巧
数据预处理
- 归一化:将输入输出缩放到[-1,1]或[0,1]区间
- 噪声添加:对训练数据加入高斯噪声,增强鲁棒性
网络结构选择
- 隐藏层数:1~3层(根据函数复杂度递增)
- 节点数量:通过网格搜索确定,初始值可设为输入节点数的2~3倍
正则化方法
- L2正则化:限制权重幅值,防止过拟合
- Dropout:随机屏蔽部分节点,提升泛化能力
激活函数选择
- 隐藏层:ReLU(加速收敛)、Leaky ReLU(缓解梯度消失)
- 输出层:线性函数(回归任务)、Sigmoid(概率输出)
训练策略
- 自适应学习率:Adam、RMSProp优化器
- 早停法(Early Stopping):验证集误差上升时终止训练
实际工程应用场景
| 领域 | 应用案例 | 拟合目标 |
|---|---|---|
| 金融预测 | 股票价格趋势预测 | 非线性时间序列函数 |
| 工业控制 | 传感器非线性校正 | 器件输入-输出特性曲线 |
| 医疗诊断 | 疾病风险评分模型 | 多参数联合分布函数 |
| 自动驾驶 | 车辆轨迹规划 | 高维状态空间映射函数 |
权威参考文献
- Simon Haykin. Neural Networks and Learning Machines (3rd Edition). Pearson, 2009.
经典教材,详解BP算法数学推导与收敛性分析
- Yann LeCun et al. Efficient BackProp. 1998.
提出权重初始化、输入预处理等加速训练方法
- Geoffrey Hinton. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. JMLR 2014.
正则化技术的里程碑式研究
通过合理设计网络结构与训练策略,BP神经网络能够逼近绝大多数工程场景中的复杂函数,实践中需结合具体问题调整参数,并通过可视化工具(如损失曲线、拟合对比图)持续优化模型性能。
















