当前位置：首页 > 行业动态 > 正文

bp神经网络 权重

BP神经网络中的权重机制解析

BP神经网络（Backpropagation Neural Network）是一种广泛应用于机器学习中的监督学习算法，其核心在于通过反向传播算法调整网络中的权重（Weights），以最小化预测误差，权重作为神经网络的关键参数，直接影响模型的性能和泛化能力，本文将深入探讨BP神经网络权重的定义、初始化、更新机制及其优化方法。

权重的定义与作用

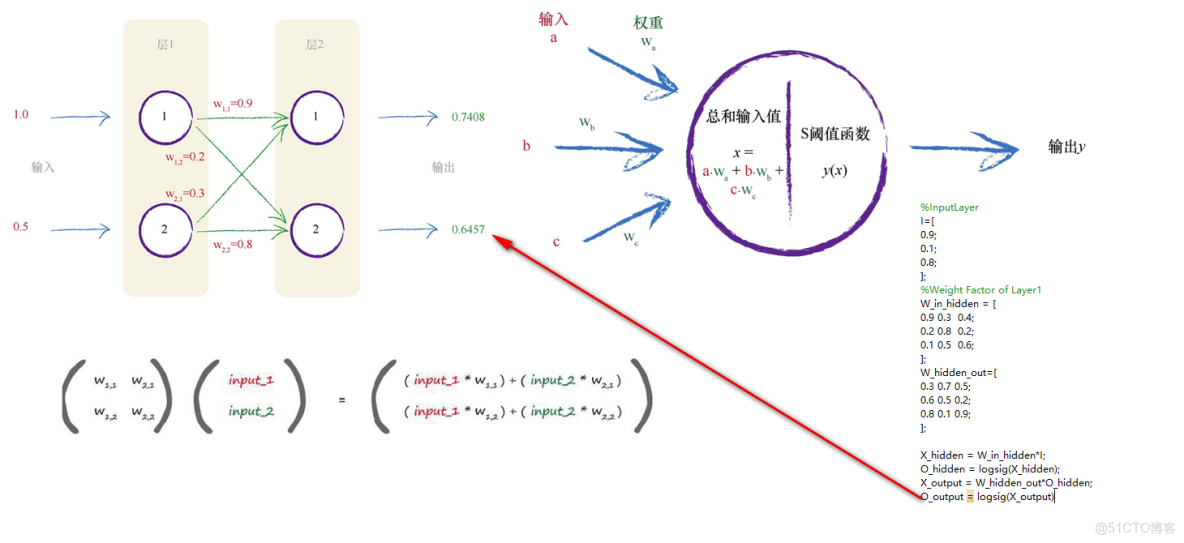
在BP神经网络中，权重是连接神经元之间的参数，用于衡量前一层神经元对后一层神经元的影响程度，以全连接网络为例，若第(l)层的第(i)个神经元与第(l+1)层的第(j)个神经元相连，则其连接权重记为(w_{ij}^{(l)})。

权重的核心作用包括：

  • 信息传递：输入数据通过权重加权求和后传递至下一层。
  • 特征提取：不同权重的组合可捕捉输入数据中的非线性特征。
  • 模型拟合：通过调整权重，使网络输出逼近真实值。

权重的初始化方法

初始权重的选择对模型训练速度和收敛性至关重要，常见初始化方法包括：

bp神经网络 权重 第1张

（1）随机初始化

  • 均匀分布：权重从([-a, a])区间内随机采样，a)取较小值（如0.01）。
  • 正态分布：权重服从均值为0、标准差为(sigma)的高斯分布。

（2）Xavier/Glorot初始化

适用于Sigmoid或Tanh激活函数，权重方差设为：
[
text{Var}(w) = frac{2}{n{text{in}} + n{text{out}}}
]
n{text{in}})和(n{text{out}})分别为输入和输出的神经元数量。

（3）He初始化

针对ReLU激活函数优化，权重方差为：
[
text{Var}(w) = frac{2}{n_{text{in}}}
]

权重的更新机制

BP神经网络通过反向传播算法更新权重，步骤如下：

  1. 前向传播：计算网络输出与真实值的误差（损失函数）。
  2. 反向传播：从输出层逐层回传误差，计算权重梯度(frac{partial L}{partial w})。
  3. 梯度下降：按学习率(eta)更新权重：
    [
    w leftarrow w – eta cdot frac{partial L}{partial w}
    ]

优化算法改进

  • 动量法（Momentum）：引入历史梯度方向，加速收敛。
  • Adam：结合动量与自适应学习率，适用于稀疏数据。

权重的正则化与优化

为防止过拟合，常对权重施加约束：

（1）L1/L2正则化

  • L1正则化：损失函数中加入(lambda sum |w|)，促进权重稀疏化。
  • L2正则化：加入(frac{lambda}{2} sum w^2)，限制权重幅度。

（2）Dropout

训练时随机丢弃部分神经元，等效于对权重进行动态平均。

常见问题与解决方案

  • 梯度消失/爆炸：
    • 使用ReLU激活函数。
    • 采用Batch Normalization。
  • 局部最优：
    • 尝试不同的初始化方法。
    • 增加随机噪声（如Simulated Annealing）。

权重是BP神经网络的“灵魂”，其初始化、更新与优化直接决定模型性能，合理选择初始化方法、优化算法及正则化策略，可显著提升训练效率和泛化能力，随着自适应权重调整技术的发展（如Meta-Learning），神经网络的应用潜力将进一步释放。

参考文献：

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
  2. Glorot, X., & Bengio, Y. (2010). Understanding the difficulty of training deep feedforward neural networks. AISTATS.
  3. He, K., et al. (2015). Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. ICCV.
0

相关文章