当前位置：首页 > 行业动态 > 正文

bp神经网络拟合

BP神经网络拟合技术详解

在人工智能和机器学习领域,BP神经网络(Back Propagation Neural Network)是一种广泛应用的多层前馈神经网络，以其强大的非线性拟合能力而闻名，本文将深入探讨BP神经网络的工作原理、拟合机制以及实际应用场景。

BP神经网络基本原理

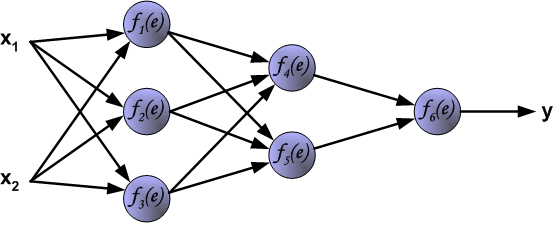
BP神经网络由输入层、隐藏层(可以有多层)和输出层组成，各层之间通过权重连接，其核心思想是通过误差反向传播算法来调整网络参数，使网络输出尽可能接近期望输出。

1 网络结构特点

  • 前向传播：输入信号从输入层经隐藏层逐层处理，最终到达输出层
  • 反向传播：根据输出误差调整各层权重和偏置
  • 激活函数：通常使用Sigmoid、Tanh或ReLU等非线性函数引入非线性特性

2 学习过程

BP神经网络的学习过程可分为四个阶段：

  1. 输入样本通过网络前向传播
  2. 计算输出与期望值的误差
  3. 误差反向传播调整权重
  4. 重复以上步骤直至误差满足要求

BP神经网络的拟合能力

BP神经网络之所以能够拟合复杂函数关系,主要基于以下数学原理：

bp神经网络拟合 第1张

1 万能逼近定理

根据Cybenko定理,一个具有单隐藏层的前馈神经网络，只要隐藏层神经元数量足够多，就能以任意精度逼近任何连续函数。

2 非线性映射能力

通过多层非线性变换,BP网络可以学习输入与输出之间复杂的非线性关系，这是线性模型无法实现的。

3 特征自动提取

隐藏层能够自动学习输入数据的有效特征表示,无需人工设计特征。

BP神经网络拟合实践

1 数据预处理

  • 归一化处理：将输入输出数据归一化到[0,1]或[-1,1]区间
  • 数据划分：通常按7:1:2分为训练集、验证集和测试集

2 网络参数设置

# 示例：使用Python构建BP神经网络
model = Sequential()
model.add(Dense(64, input_dim=8, activation='relu'))  # 隐藏层
model.add(Dense(32, activation='relu'))              # 隐藏层
model.add(Dense(1, activation='linear'))             # 输出层
model.compile(loss='mse', optimizer='adam')          # 损失函数和优化器

3 训练技巧

  • 学习率调整：初始学习率通常设为0.001-0.01
  • 早停机制：验证集误差不再下降时停止训练
  • 正则化：使用L1/L2正则化防止过拟合
  • 批量归一化：加速训练过程

BP神经网络拟合的挑战与解决方案

1 常见问题

  1. 过拟合：网络在训练集表现良好但泛化能力差
  2. 局部极小值：陷入非全局最优解
  3. 梯度消失/爆炸：深层网络训练困难

2 应对策略

  • Dropout：随机丢弃部分神经元防止过拟合
  • 自适应优化器：如Adam、RMSprop等
  • 残差连接：解决深层网络梯度消失问题
  • 集成学习：结合多个网络模型提高稳定性

BP神经网络在实际中的应用

BP神经网络因其强大的拟合能力,在多个领域得到广泛应用：

  1. 金融预测：股票价格预测、信用评分
  2. 工业控制：过程优化、故障诊断
  3. 医疗诊断：疾病预测、医学图像分析
  4. 自然语言处理：文本分类、情感分析
  5. 计算机视觉：图像识别、目标检测

BP神经网络的发展趋势

随着深度学习的发展,BP神经网络也在不断演进：

  • 与卷积神经网络(CNN)结合处理图像数据
  • 与循环神经网络(RNN)结合处理时序数据
  • 注意力机制的引入提高特征提取能力
  • 轻量化设计适应移动端部署

BP神经网络作为经典的机器学习模型,其强大的非线性拟合能力使其在众多领域持续发挥作用，理解其工作原理和优化方法，对于实际应用中的模型选择和调优至关重要，随着计算能力的提升和算法的改进，BP神经网络仍将在人工智能领域保持重要地位。

参考文献：

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.
  2. Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of control, signals and systems, 2(4), 303-314.
  3. 周志华. (2016). 机器学习. 清华大学出版社.
0

相关文章