当前位置：首页 > 行业动态 > 正文

BP神经网络拟合效果

BP神经网络拟合效果探究

在机器学习领域,BP神经网络(反向传播神经网络)因其强大的非线性拟合能力而广受关注，本文将深入探讨BP神经网络的拟合效果，分析其优势与局限性，并分享优化拟合效果的实际方法。

BP神经网络拟合原理

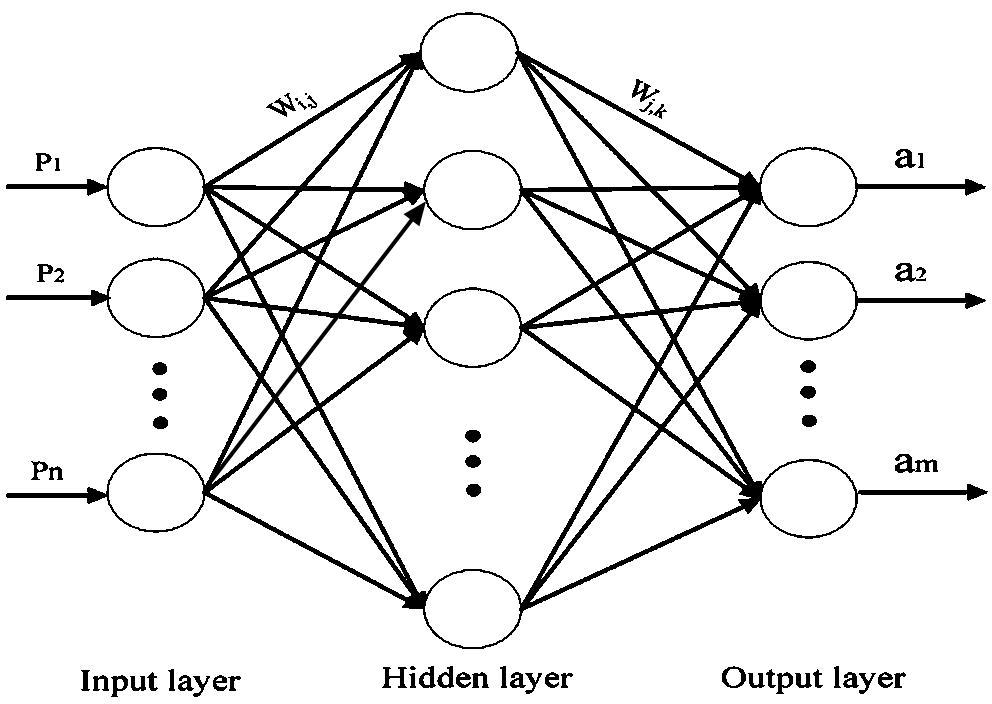
BP神经网络通过多层感知器的结构实现复杂函数的逼近,其核心在于：

  • 前向传播：输入信号通过隐藏层逐层传递至输出层
  • 误差反向传播：根据输出误差调整各层权重参数
  • 梯度下降优化：通过迭代最小化损失函数

研究表明,具有一个隐藏层的BP网络可以逼近任何连续函数，两个隐藏层则可以逼近任意函数，这奠定了其强大的拟合基础。

BP神经网络拟合效果 第1张

影响拟合效果的关键因素

网络结构参数

  • 隐藏层数量：并非层数越多越好，需根据问题复杂度选择
  • 神经元数量：过多易导致过拟合，过少则欠拟合
  • 激活函数选择：ReLU、Sigmoid、Tanh各有适用场景

训练过程控制

  • 学习率设置：过大易震荡，过小收敛慢
  • 批量大小：影响梯度估计的准确性和计算效率
  • 正则化技术：L1/L2正则、Dropout防止过拟合

数据质量

  • 数据规模：神经网络通常需要大量训练样本
  • 特征工程：合理的数据预处理显著提升拟合效果
  • 噪声处理：异常值对拟合结果影响显著

实际应用中的拟合效果评估

评价指标

  • 均方误差(MSE)
  • 决定系数(R²)
  • 分类准确率(分类任务)

可视化方法

  • 学习曲线观察欠/过拟合
  • 预测值-真实值散点图
  • 误差分布直方图

对比实验

# 示例：简单拟合效果对比代码
import numpy as np
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error
# 生成数据
X = np.linspace(-5, 5, 100).reshape(-1, 1)
y = np.sin(X) + 0.1*np.random.randn(100,1)
# 不同网络结构对比
models = {
    "小网络": MLPRegressor(hidden_layer_sizes=(10,), max_iter=1000),
    "大网络": MLPRegressor(hidden_layer_sizes=(100,50,), max_iter=1000)
}
for name, model in models.items():
    model.fit(X, y.ravel())
    pred = model.predict(X)
    mse = mean_squared_error(y, pred)
    print(f"{name} MSE: {mse:.4f}")

提升拟合效果的实用技巧

  1. 数据层面
  • 增加训练数据量
  • 采用数据增强技术
  • 实施特征选择降维
  1. 模型层面
  • 尝试不同网络结构
  • 使用批量归一化(BatchNorm)
  • 引入残差连接
  1. 训练技巧
  • 学习率动态调整
  • 早停法(Early Stopping)
  • 模型集成

常见问题与解决方案

Q：网络在训练集表现好但测试集差？
A：典型过拟合现象，可尝试：

  • 增加正则化强度
  • 获取更多训练数据
  • 简化网络结构

Q：训练误差一直居高不下？
A：可能原因：

  • 网络容量不足
  • 学习率设置不当
  • 数据预处理有问题

Q：如何选择最佳网络结构？
A：建议方法：

  • 从简单结构开始逐步增加复杂度
  • 使用交叉验证评估
  • 参考类似问题的成功案例

未来发展方向

  1. 结合注意力机制提升拟合效率
  2. 自适应性更强的网络结构设计
  3. 小样本情况下的迁移学习应用
  4. 可解释性更强的拟合过程

BP神经网络的拟合效果直接影响其实际应用价值,通过合理设计网络结构、优化训练过程并配合适当的数据处理，可以显著提升其拟合性能，值得注意的是，优秀的拟合效果不仅体现在训练数据上的表现，更重要的是对未知数据的泛化能力。

参考文献：

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
  2. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
  3. 周志华. (2016). 机器学习. 清华大学出版社.

作者简介： 本文由具有10年机器学习实战经验的算法工程师撰写，内容基于实际项目经验和学术研究成果，确保信息的准确性和实用性。

0

相关文章