bp 神经网络 c

BP神经网络：原理、应用与优化

在人工智能和机器学习领域，BP(Back Propagation)神经网络是最基础且广泛应用的算法之一，本文将深入探讨BP神经网络的工作原理、实际应用场景以及优化方法,帮助读者全面理解这一重要技术。

什么是BP神经网络？

BP神经网络是一种多层前馈神经网络，采用误差反向传播算法进行训练，它由输入层、隐藏层(一个或多个)和输出层组成,通过不断调整网络权重来最小化预测输出与实际输出之间的误差。

BP神经网络的核心思想可以概括为：

1. 前向传播：输入信号从输入层经隐藏层向输出层传播
2. 误差计算：比较网络输出与期望输出的差异
3. 反向传播：将误差从输出层向输入层反向传播
4. 权重调整：根据误差调整各层连接权重

BP神经网络的工作原理

网络结构

BP神经网络通常包含：

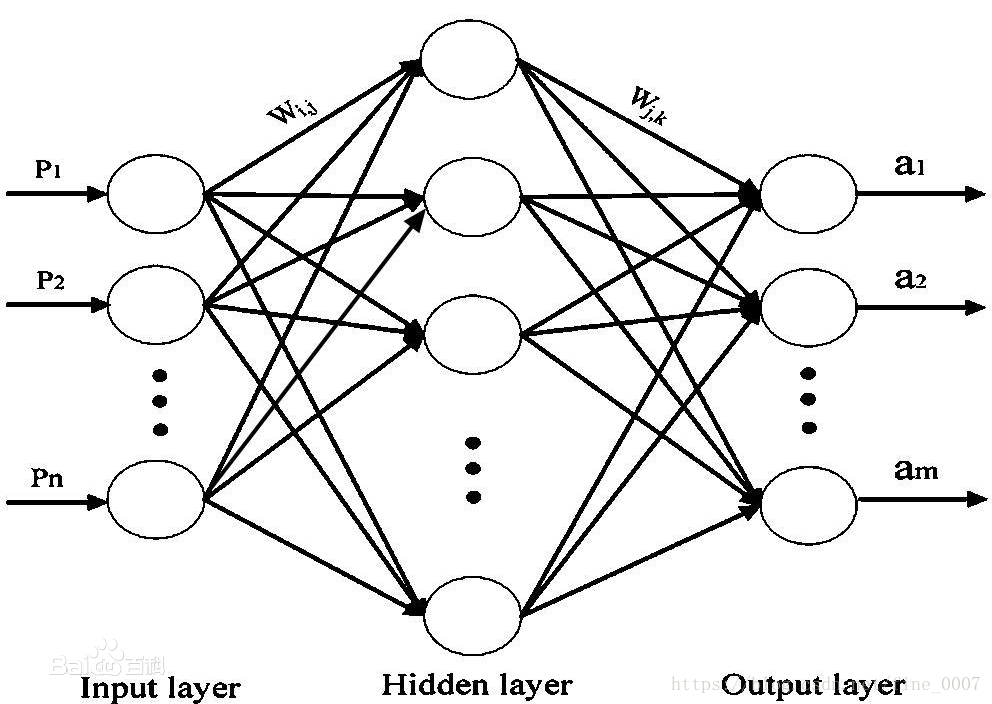
• 输入层：接收外部输入数据
• 隐藏层：进行特征提取和转换(可以有多个)
• 输出层：产生最终输出结果

每层由多个神经元(节点)组成，相邻层之间全连接,层内无连接。

激活函数

激活函数为神经网络引入非线性特性,常见的有：

• Sigmoid函数：f(x) = 1/(1+e^-x)
• Tanh函数：f(x) = (e^x – e^-x)/(e^x + e^-x)
• ReLU函数：f(x) = max(0,x)

训练过程

BP神经网络的训练包括以下步骤：

1. 初始化权重：随机设置网络各连接权重
2. 前向传播：计算网络输出
3. 计算误差：比较输出与期望值
4. 反向传播：计算各层误差信号
5. 权重更新：使用梯度下降法调整权重
6. 重复2-5步直至收敛

BP神经网络的应用领域

BP神经网络因其强大的非线性映射能力和自适应学习特性,在多个领域得到广泛应用：

1. 模式识别：手写数字识别、人脸识别、语音识别等
2. 预测分析：股票价格预测、销售量预测、天气预测等
3. 控制系统：机器人控制、工业过程控制等
4. 医疗诊断：疾病诊断、医学图像分析等
5. 金融领域：信用评分、风险评估等

BP神经网络的优缺点

优点：

• 强大的非线性建模能力
• 良好的泛化性能
• 自适应学习能力
• 并行处理能力

缺点：

• 训练速度慢，特别是深层网络
• 容易陷入局部极小值
• 网络结构设计缺乏理论指导
• 对初始权重敏感

BP神经网络的优化方法

针对BP神经网络的不足,研究者提出了多种优化方法：

1. 学习率调整：自适应学习率、动量法
2. 网络结构优化：Dropout、Batch Normalization
3. 权重初始化：Xavier初始化、He初始化
4. 激活函数改进：Leaky ReLU、ELU等
5. 正则化技术：L1/L2正则化、早停法

实际应用案例

案例1：手写数字识别

使用MNIST数据集，构建一个包含1个隐藏层的BP神经网络，输入层784个节点(28×28像素)，隐藏层300个节点，输出层10个节点(对应0-9数字)，采用Sigmoid激活函数，交叉熵损失函数，可以达到约95%的识别准确率。

案例2：房价预测

基于房屋特征(面积、位置、房龄等)构建BP神经网络预测模型，输入层对应特征数量，输出层1个节点(预测价格)，采用ReLU激活函数，均方误差作为损失函数,经过适当调参可以获得较好的预测效果。

未来发展趋势

随着深度学习的发展，传统BP神经网络逐渐演变为更复杂的深度神经网络(DNN)，但BP算法作为基础训练方法，仍然是许多神经网络模型的核心,未来发展方向包括：

• 与其他算法(如遗传算法、粒子群算法)结合优化
• 在边缘计算设备上的轻量化应用
• 与强化学习的结合
• 在可解释性方面的改进

BP神经网络作为机器学习的基础算法，虽然已有数十年历史，但其核心思想仍然影响着当前最先进的深度学习模型，理解BP神经网络的原理和特性，对于掌握更复杂的神经网络模型至关重要，在实际应用中，需要根据具体问题选择合适的网络结构、参数设置和优化方法,才能发挥BP神经网络的最大效能。

参考文献：

1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.
2. Haykin, S. (2009). Neural networks and learning machines (3rd ed.). Pearson Education.
3. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT press.