当前位置：首页 > 行业动态 > 正文

bp神经网络神经网络节点

BP神经网络节点解析

神经网络节点的基本概念

在BP神经网络中，节点(也称为神经元)是构成网络的基本单元，每个节点接收来自前一层节点的输入信号，经过加权求和后通过激活函数处理，最终输出到下一层节点,节点的数量和排列方式直接影响着神经网络的性能和复杂度。

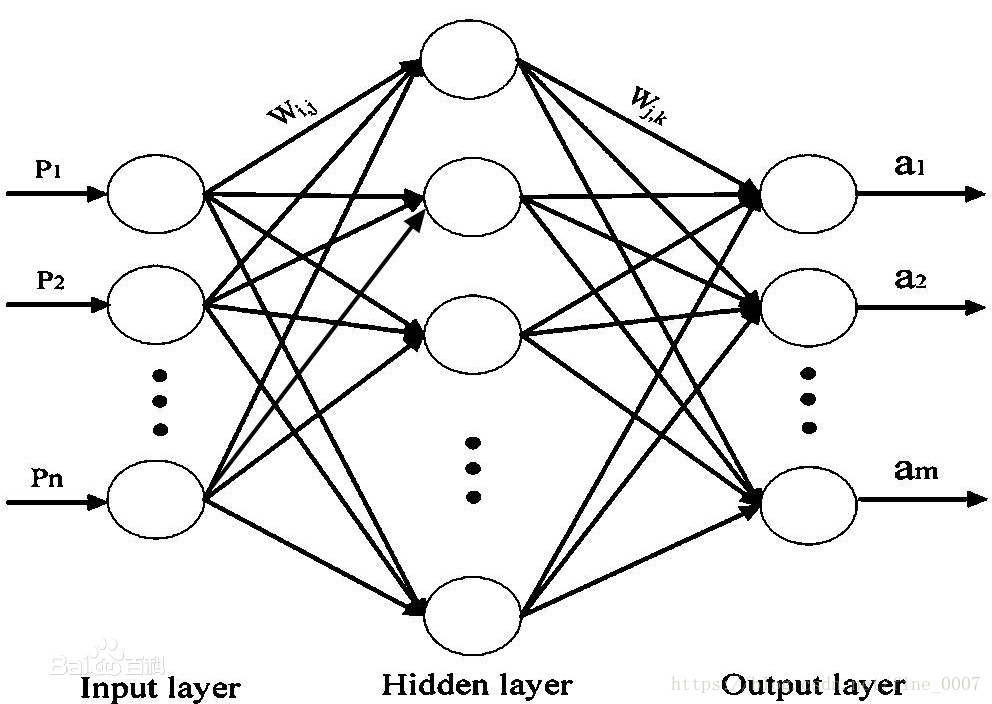
典型的BP神经网络包含三种类型的节点：

  1. 输入层节点：负责接收外部输入数据
  2. 隐藏层节点：负责中间信息处理和特征提取
  3. 输出层节点：产生最终的预测或分类结果

节点的工作原理

每个神经网络节点执行以下数学运算：

输出 = 激活函数(∑(权重×输入) + 偏置)
  • 权重(Weight)：决定输入信号的重要性
  • 偏置(Bias)：调整节点的激活阈值
  • 激活函数：引入非线性因素，使网络能够学习复杂模式

激活函数的选择

常见的激活函数及其特性：

  1. Sigmoid函数：

    • 公式：f(x) = 1 / (1 + e^(-x))
    • 输出范围(0,1)，适合概率输出
    • 存在梯度消失问题

  2. Tanh函数：

    • 公式：f(x) = (e^x – e^(-x)) / (e^x + e^(-x))
    • 输出范围(-1,1)，中心对称
    • 同样存在梯度消失问题

  3. ReLU函数：

    • 公式：f(x) = max(0,x)
    • 计算简单，缓解梯度消失
    • 可能出现”神经元死亡”问题

  4. Leaky ReLU：

    • 公式：f(x) = max(αx,x)，为小正数
    • 解决ReLU的神经元死亡问题

节点数量的确定

确定每层节点数量是网络设计的关键：

bp神经网络神经网络节点 第1张

  1. 输入层节点数：

    • 通常等于输入特征的维度
    • 处理28×28图像时，可展平为784个输入节点

  2. 隐藏层节点数：

    • 没有固定公式，通常通过实验确定
    • 常见经验法则：
      • 介于输入和输出层节点数之间
      • 使用网格搜索或随机搜索优化
      • 考虑网络容量与过拟合的平衡

  3. 输出层节点数：

    • 分类问题：通常等于类别数量
    • 回归问题：通常为1个或多个预测值

节点的训练过程

BP神经网络通过反向传播算法训练节点参数：

  1. 前向传播：计算网络输出
  2. 计算损失函数：比较输出与真实值
  3. 反向传播：从输出层到输入层逐层计算梯度
  4. 参数更新：使用梯度下降法调整权重和偏置

关键训练参数：

  • 学习率：控制参数更新步长
  • 批量大小：每次迭代使用的样本数
  • 正则化：防止过拟合(如L1/L2正则化)

节点优化的高级技术

  1. 批量归一化(Batch Normalization)：

    • 对每层的输入进行标准化
    • 加速训练，允许使用更高学习率

  2. Dropout技术：

    • 训练时随机”丢弃”部分节点
    • 有效防止过拟合

  3. 权重初始化策略：

    • Xavier初始化：适合Sigmoid/Tanh
    • He初始化：适合ReLU及其变体

  4. 自适应优化算法：

    • Adam：结合动量与自适应学习率
    • RMSprop：自适应调整学习率

实际应用中的节点设计

  1. 结构化数据建模：

    • 输入节点对应特征字段
    • 隐藏层节点数逐步递减

  2. 图像处理：

    • 全连接节点可能效率低下
    • 通常结合卷积神经网络(CNN)

  3. 序列数据处理：

    • 考虑循环神经网络(RNN)结构
    • 节点需具备记忆功能

常见问题与解决方案

  1. 过拟合：

    • 增加Dropout层
    • 使用L1/L2正则化
    • 获取更多训练数据

  2. 欠拟合：

    • 增加网络深度或宽度
    • 减少正则化强度
    • 延长训练时间

  3. 梯度消失/爆炸：

    • 使用ReLU等激活函数
    • 实施梯度裁剪
    • 采用残差连接

未来发展趋势

  1. 自动化节点设计：

    • 神经架构搜索(NAS)
    • 自动化机器学习(AutoML)

  2. 新型节点结构：

    • 胶囊网络(Capsule Networks)
    • 注意力机制节点

  3. 生物启发节点：

    • 脉冲神经网络(SNN)
    • 更接近生物神经元的行为

参考文献：

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
  2. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
  3. Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
0

相关文章