当前位置：首页 > 行业动态 > 正文

bp神经网络程序代码注释

bp神经网络程序代码注释 第1张

BP神经网络程序代码注释

导入必要的库

import numpy as np  # 用于数值计算的基础库
import matplotlib.pyplot as plt  # 用于绘制图形和可视化

定义Sigmoid激活函数及其导数

def sigmoid(x):
    """
    Sigmoid激活函数
    参数:
        x: 输入值
    返回:
        经过Sigmoid函数处理后的值，范围在(0,1)之间
    """
    return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
    """
    Sigmoid函数的导数
    参数:
        x: 输入值
    返回:
        Sigmoid函数在x处的导数值
    """
    return x * (1 - x)

神经网络类定义

class NeuralNetwork:
    def __init__(self, x, y):
        """
        神经网络初始化
        参数:
            x: 输入数据
            y: 期望输出
        """
        self.input = x  # 存储输入数据
        self.weights1 = np.random.rand(self.input.shape[1],4)  # 第一层权重矩阵，随机初始化
        self.weights2 = np.random.rand(4,1)  # 第二层权重矩阵，随机初始化
        self.y = y  # 存储期望输出
        self.output = np.zeros(y.shape)  # 初始化输出矩阵
    def feedforward(self):
        """
        前向传播过程
        计算神经网络的输出
        """
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))  # 计算隐藏层输出
        self.output = sigmoid(np.dot(self.layer1, self.weights2))  # 计算最终输出
    def backprop(self):
        """
        反向传播过程
        根据误差调整权重
        """
        # 计算输出层和隐藏层的误差
        d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * 
                          sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T, (np.dot(2*(self.y - self.output) * 
                          sigmoid_derivative(self.output), self.weights2.T) * 
                          sigmoid_derivative(self.layer1)))
        # 更新权重
        self.weights1 += d_weights1
        self.weights2 += d_weights2
    def train(self, epochs):
        """
        训练神经网络
        参数:
            epochs: 训练迭代次数
        """
        loss_history = []  # 存储损失值历史记录
        for i in range(epochs):
            self.feedforward()  # 前向传播
            self.backprop()  # 反向传播
            # 计算并记录损失值(均方误差)
            loss = np.mean(np.square(self.y - self.output))
            loss_history.append(loss)
            # 每1000次迭代打印一次损失值
            if i % 1000 == 0:
                print(f"迭代次数: {i}, 损失值: {loss}")
        return loss_history

示例使用

if __name__ == "__main__":
    # 定义训练数据
    X = np.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]])  # 输入数据
    y = np.array([[0],[1],[1],[0]])  # 期望输出(XOR问题)
    # 创建神经网络实例
    nn = NeuralNetwork(X, y)
    # 训练神经网络(10000次迭代)
    loss_history = nn.train(10000)
    # 打印最终预测结果
    print("n最终预测结果:")
    print(nn.output)
    # 绘制损失值变化曲线
    plt.figure(figsize=(10,6))
    plt.plot(loss_history)
    plt.title('训练过程中的损失值变化')
    plt.xlabel('迭代次数')
    plt.ylabel('损失值')
    plt.grid(True)
    plt.show()

代码功能说明

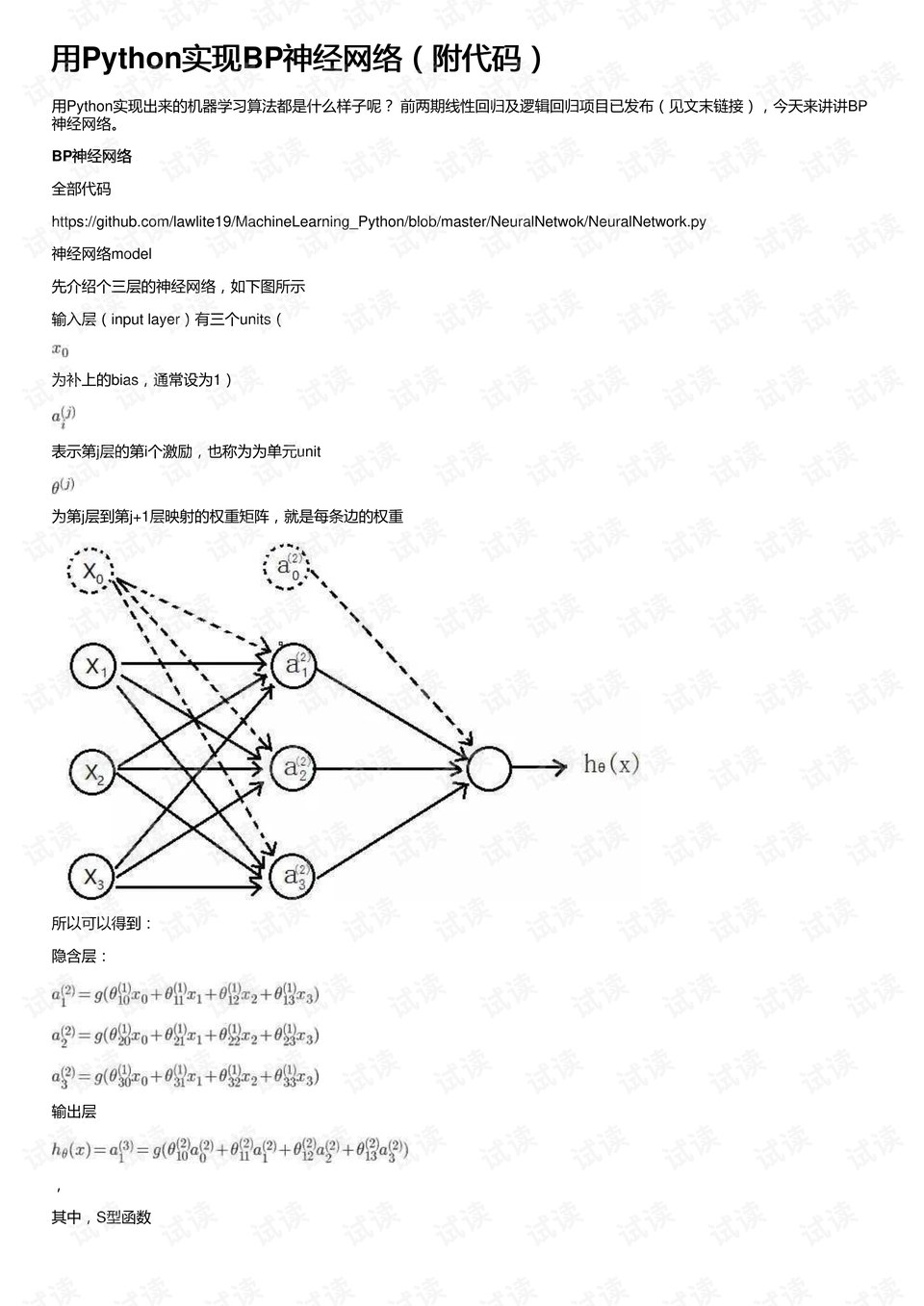
  1. 神经网络结构：实现了一个简单的三层BP神经网络(输入层、隐藏层、输出层)
  2. 激活函数：使用Sigmoid作为激活函数，并实现了其导数计算
  3. 训练过程：包含完整的前向传播和反向传播过程
  4. 损失跟踪：记录并可视化训练过程中的损失值变化
  5. 应用示例：解决了一个简单的XOR问题

注意事项

  1. 学习率未显式设置,实际应用中可能需要调整
  2. 隐藏层节点数固定为4,可根据问题复杂度调整
  3. 权重初始化采用随机方法,可能影响训练效果
  4. 对于更复杂的问题,可能需要增加网络层数或节点数

参考文献

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.
  2. Nielsen, M. A. (2015). Neural Networks and Deep Learning. Determination Press.
  3. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
0

相关文章