当前位置：首页 > 行业动态 > 正文

bp神经网络性能函数

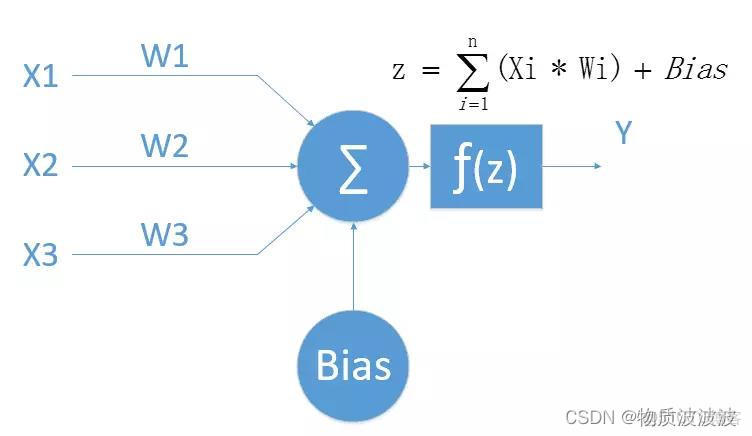
BP神经网络性能函数

BP神经网络(Back Propagation Neural Network)的性能函数是衡量网络输出与期望输出之间差异的重要指标，直接影响着网络的训练效果和最终性能，作为神经网络的核心组成部分，性能函数的选择对模型收敛速度、泛化能力和最终精度都有着决定性作用。

常见性能函数类型

均方误差函数(MSE)

均方误差(Mean Squared Error)是最常用的性能函数之一,计算公式为：

MSE = 1/n * Σ(y_true - y_pred)^2

其中n为样本数量，y_true为真实值，y_pred为预测值，MSE对较大误差给予更高惩罚,适用于大多数回归问题。

交叉熵损失函数

交叉熵(Cross Entropy)损失函数特别适合分类问题,尤其当输出为概率分布时：

bp神经网络性能函数 第1张

CE = -Σ(y_true * log(y_pred))

二分类问题常使用二元交叉熵,多分类问题则使用分类交叉熵。

绝对平均误差函数(MAE)

绝对平均误差(Mean Absolute Error)计算预测值与真实值之差的绝对值：

MAE = 1/n * Σ|y_true - y_pred|

MAE对异常值不如MSE敏感,在存在离群点的数据中表现更稳健。

性能函数选择原则

  1. 问题类型匹配：回归问题通常选择MSE或MAE，分类问题优先考虑交叉熵
  2. 数据特性考量：数据含噪声或异常值时，MAE可能优于MSE
  3. 训练效率：不同性能函数可能导致收敛速度差异
  4. 输出范围：确保性能函数输出与激活函数范围兼容

性能函数优化技巧

  1. 正则化项添加：L1/L2正则化防止过拟合
  2. 自定义损失函数：针对特定业务需求设计
  3. 多目标权衡：多个性能函数的加权组合
  4. 动态调整策略：训练过程中根据表现调整

实际应用中的注意事项

  1. 性能函数值突然增大可能预示梯度爆炸
  2. 长期不下降可能意味着陷入局部最优
  3. 验证集性能比训练集性能更能反映泛化能力
  4. 不同性能函数之间比较需谨慎，数值范围可能不同

性能评估指标

除了训练时的性能函数,还应关注：

  • 准确率(Accuracy)
  • 精确率(Precision)
  • 召回率(Recall)
  • F1分数
  • ROC曲线下面积(AUC)

这些指标从不同角度评估模型性能,应与性能函数配合使用。

BP神经网络性能函数的选择和优化是一门需要理论与实践结合的学问，优秀的机器学习工程师不仅需要了解各种性能函数的数学特性，更要具备根据实际问题灵活选择和调整的能力，随着深度学习的发展，新型性能函数不断涌现,但基本原理和选择策略仍然适用。

参考文献：

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.
  2. Bishop, C. M. (1995). Neural networks for pattern recognition. Oxford university press.
  3. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT press.
0

相关文章