当前位置：首页 > 行业动态 > 正文

bp神经网络 最后一层

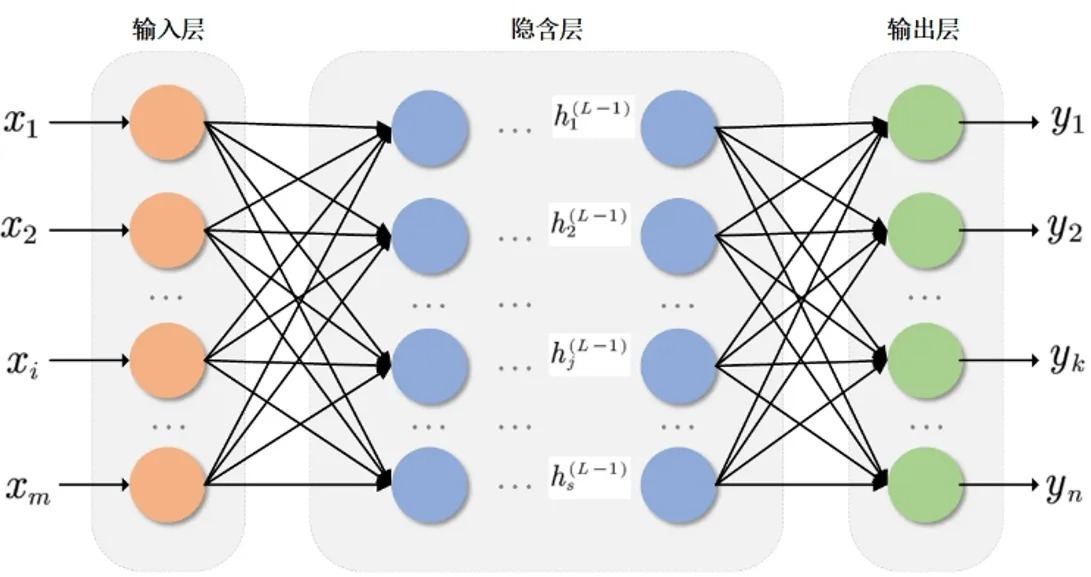
BP神经网络最后一层详解

BP(Back Propagation)神经网络的最后一层是整个网络架构中最为关键的部分之一，它直接决定了网络的输出形式和性能表现，本文将深入解析BP神经网络最后一层的设计原理、常见类型以及在实际应用中的选择策略。

最后一层的基本功能

BP神经网络的最后一层主要承担以下核心功能：

  1. 输出转换：将前一层传递来的特征表示转换为最终需要的输出形式
  2. 损失计算：为反向传播提供误差信号的基础
  3. 任务适配：根据具体任务(分类、回归等)调整输出特性

最后一层的神经元数量通常与任务需求直接相关,二分类问题通常使用1个输出神经元，多分类问题则使用与类别数相等的输出神经元。

常见最后一层结构类型

线性输出层

适用场景：回归问题、无约束输出

线性输出层是最简单的形式,直接输出加权和的线性组合：

z = W·a + b

其中W是权重矩阵,a是上一层的激活输出，b是偏置项，这种结构不施加任何非线性变换，适用于输出值范围不受限制的回归任务。

Sigmoid输出层

适用场景：二分类问题、概率输出

Sigmoid函数将输出压缩到(0,1)区间，公式为：

bp神经网络 最后一层 第1张

σ(z) = 1 / (1 + e^{-z})

这种结构特别适合二分类问题,可以直观地解释为属于正类的概率，在多层感知机中，Sigmoid曾经是隐藏层和输出层的标准选择，但现在多限于输出层使用。

Softmax输出层

适用场景：多分类问题

Softmax函数是多分类问题的标准选择,它将输出转换为概率分布：

softmax(z)_i = e^{z_i} / Σ_j e^{z_j}

每个输出代表一个类别的概率,所有输出之和为1，这种结构与交叉熵损失函数配合使用效果最佳。

Tanh输出层

适用场景：输出范围在[-1,1]的回归问题

Tanh函数将输出压缩到(-1,1)区间：

tanh(z) = (e^z - e^{-z}) / (e^z + e^{-z})

相比Sigmoid,Tanh的输出以0为中心，在某些回归任务中表现更好。

最后一层的设计考量

与损失函数的匹配

最后一层的选择必须与损失函数协调：

  • 线性输出层通常配MSE(均方误差)损失
  • Sigmoid输出层配二元交叉熵损失
  • Softmax输出层配分类交叉熵损失
  • Tanh输出层也可配MSE损失

初始化策略

最后一层的权重初始化需要特别注意：

  • Sigmoid/Softmax输出层：建议使用较小的初始权重(如Xavier初始化)
  • 线性输出层：可以使用标准正态分布初始化
  • 避免过大初始权重导致梯度消失

正则化应用

最后一层同样需要正则化防止过拟合：

  • L1/L2权重正则化
  • Dropout(谨慎使用，可能影响输出质量)
  • 早停法(Early Stopping)

实践建议

  1. 分类问题：优先考虑Softmax(多类)或Sigmoid(二类)输出层
  2. 回归问题：简单问题用线性输出层，有界输出用Sigmoid/Tanh
  3. 多标签分类：可以使用多个Sigmoid输出神经元
  4. 不平衡数据：考虑在损失函数中引入类别权重

常见问题解决方案

梯度消失问题

在深层网络中,Sigmoid/Tanh输出层可能导致梯度消失，解决方案：

  • 使用ReLU等激活函数的隐藏层
  • 残差连接
  • 批归一化

输出饱和问题

当Sigmoid/Softmax输出接近0或1时，梯度会变得极小，解决方案：

  • 谨慎初始化权重
  • 使用交叉熵损失而非MSE
  • 加入小的噪声

多任务学习

对于需要同时输出多种类型结果的任务(如既分类又回归)，可以设计多个并行输出层，每个采用适合其任务的结构。

前沿发展

近年来,最后一层设计也有一些新趋势：

  1. 自适应Softmax：加速大规模分类问题
  2. 标签平滑：防止模型对标签过度自信
  3. 温度缩放：调整Softmax的”软硬”程度
  4. 能量基模型：替代传统概率输出

BP神经网络的最后一层是连接模型与具体任务的桥梁,其设计直接影响模型性能，合理选择输出层类型、匹配适当的损失函数、采用正确的初始化策略，都是构建高效神经网络的关键，随着深度学习的发展，输出层的设计也在不断创新，但基本原理仍然建立在传统的BP算法基础之上。

参考文献：

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
  2. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
  3. Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
0

相关文章