当前位置：首页 > 行业动态 > 正文

bp神经网络求权重

BP神经网络求权重

在机器学习和人工智能领域，反向传播(BP)神经网络是最基础且应用广泛的模型之一，权重作为神经网络的核心参数，直接影响模型的预测能力和学习效果，本文将深入探讨BP神经网络中权重的求解原理、方法和实际应用。

神经网络权重基础概念

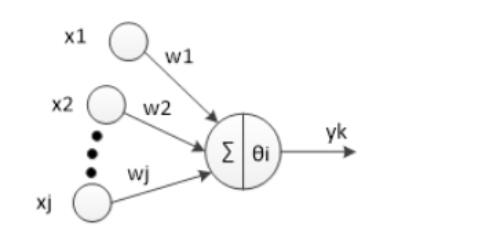
神经网络由大量相互连接的神经元组成，每个连接都有一个权重值，表示信号传递的强度,权重决定了输入信号对神经元激活程度的影响大小。

权重矩阵W可以表示为：

W = [w₁₁ w₁₂ ... w₁ₙ
     w₂₁ w₂₂ ... w₂ₙ
     ... ... ... ...
     wₘ₁ wₘ₂ ... wₘₙ]

其中wᵢⱼ表示第i个神经元与第j个神经元之间的连接权重。

权重初始化方法

良好的权重初始化对神经网络训练至关重要：

  1. 随机初始化：从均匀分布或正态分布中随机采样

    # 均匀分布初始化
W = np.random.uniform(-1, 1, size=(input_dim, output_dim))
# 正态分布初始化
W = np.random.normal(0, 0.1, size=(input_dim, output_dim))

  2. Xavier/Glorot初始化：考虑输入输出维度

    limit = np.sqrt(6 / (input_dim + output_dim))
W = np.random.uniform(-limit, limit, (input_dim, output_dim))

  3. He初始化：适用于ReLU激活函数

    bp神经网络求权重 第1张

    std = np.sqrt(2 / input_dim)
W = np.random.normal(0, std, (input_dim, output_dim))

反向传播算法求权重

反向传播算法通过梯度下降优化权重,主要步骤如下：

  1. 前向传播：计算网络输出

    z = W·x + b
a = σ(z)

  2. 计算损失函数：如均方误差(MSE)

    L = 1/2Σ(y - ŷ)²

  3. 反向传播误差：链式法则求梯度

    ∂L/∂W = ∂L/∂ŷ · ∂ŷ/∂z · ∂z/∂W

  4. 权重更新：学习率η控制步长

    W = W - η·∂L/∂W

权重优化进阶方法

  1. 动量法(Momentum)：积累历史梯度

    v = γv + η∇W
W = W - v

  2. Adam优化器：自适应学习率

    m = β₁m + (1-β₁)∇W
v = β₂v + (1-β₂)(∇W)²
W = W - η·m/(√v + ε)

  3. 学习率衰减：训练后期减小步长

    η = η₀/(1 + decay_rate×epoch)

权重正则化技术

防止过拟合的常用方法：

  1. L2正则化(权重衰减)

    L = L₀ + λ/2Σw²

  2. L1正则化

    L = L₀ + λΣ|w|

  3. Dropout：随机屏蔽神经元

    mask = (np.random.rand(*W.shape) < p) / p
W = W * mask

实际应用注意事项

  1. 梯度消失/爆炸问题：使用Batch Normalization或残差连接
  2. 权重可视化：监控训练过程中权重的分布变化
  3. 权重共享：在CNN等架构中复用权重
  4. 迁移学习：预训练权重微调(Fine-tuning)

代码实现示例

import numpy as np
class NeuralNetwork:
    def __init__(self, layers):
        self.weights = []
        for i in range(len(layers)-1):
            # He初始化
            std = np.sqrt(2/layers[i])
            W = np.random.normal(0, std, (layers[i], layers[i+1]))
            self.weights.append(W)
    def forward(self, X):
        self.activations = [X]
        for W in self.weights:
            X = np.dot(X, W)
            X = self.relu(X)  # ReLU激活函数
            self.activations.append(X)
        return X
    def backward(self, X, y, learning_rate=0.01):
        # 计算梯度
        m = X.shape[0]
        error = self.activations[-1] - y
        deltas = [error * self.relu_derivative(self.activations[-1])]
        # 反向传播误差
        for i in range(len(self.weights)-1, 0, -1):
            delta = np.dot(deltas[-1], self.weights[i].T) * 
                    self.relu_derivative(self.activations[i])
            deltas.append(delta)
        deltas.reverse()
        # 更新权重
        for i in range(len(self.weights)):
            grad = np.dot(self.activations[i].T, deltas[i]) / m
            self.weights[i] -= learning_rate * grad
    def relu(self, x):
        return np.maximum(0, x)
    def relu_derivative(self, x):
        return (x > 0).astype(float)

常见问题解答

Q：为什么需要反向传播求权重？
A：神经网络有大量参数，手动设置不现实，反向传播通过自动计算梯度,高效优化权重。

Q：权重初始化为零会怎样？
A：导致所有神经元学习相同的特征，破坏网络的对称性破坏机制,严重影响学习能力。

Q：如何判断权重是否合理？
A：监控训练/验证损失曲线，检查权重分布直方图,观察模型在测试集的表现。

参考文献

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
  2. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
  3. Glorot, X., & Bengio, Y. (2010). Understanding the difficulty of training deep feedforward neural networks. AISTATS.
  4. Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
0

相关文章