bp神经网络程序

BP神经网络程序：核心原理与实现步骤

BP神经网络（Backpropagation Neural Network）是一种基于误差反向传播算法的多层前馈神经网络，广泛应用于分类、回归、模式识别等领域，其核心思想是通过不断调整网络权重与偏置，使模型输出与实际值之间的误差最小化,以下是关于BP神经网络程序的详细解析：

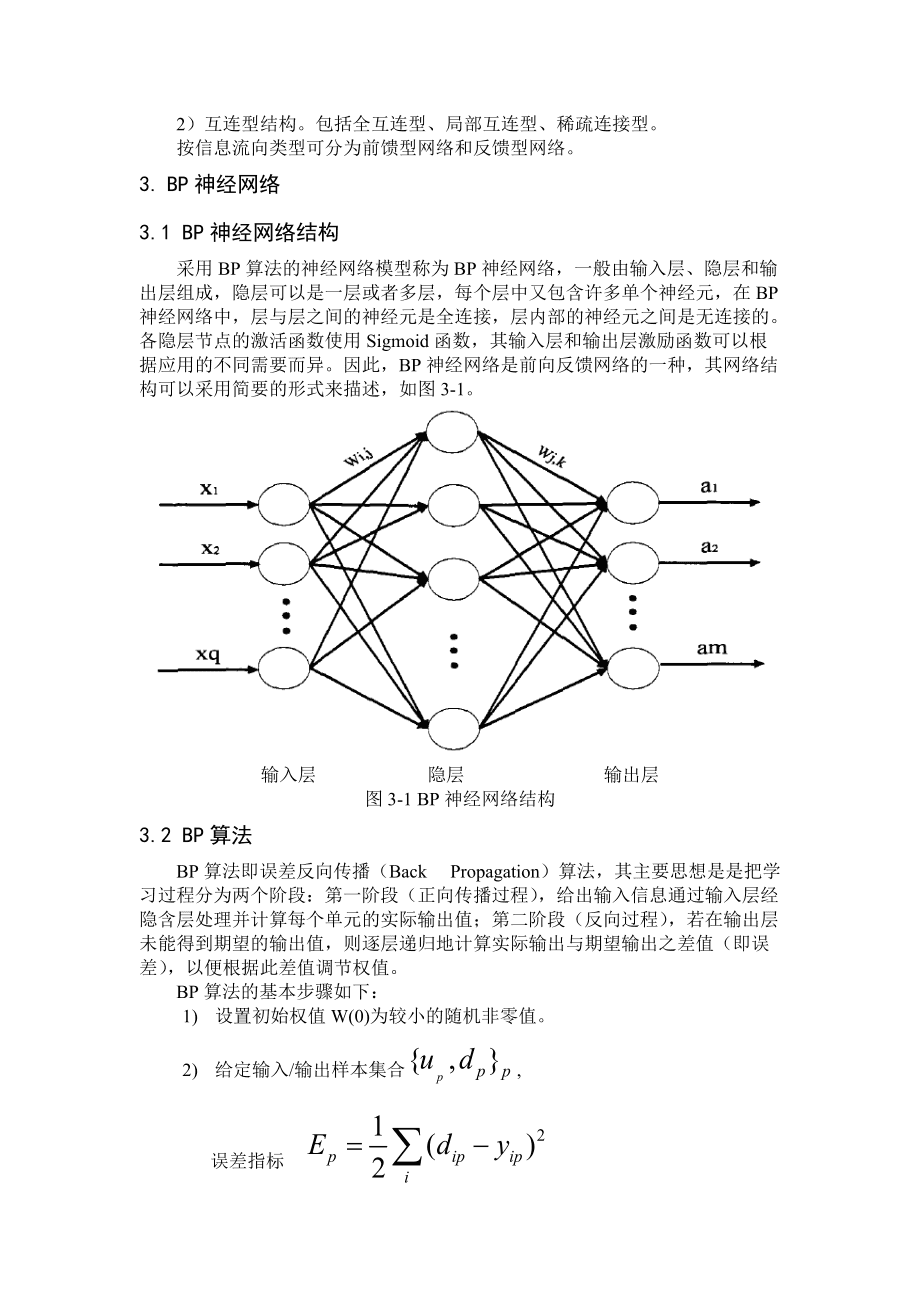
BP神经网络的核心原理

1. 网络结构
   BP神经网络通常包含三层结构：

   • 输入层：接收原始数据（如图像像素、传感器数据）。
   • 隐含层：通过激活函数（如Sigmoid、ReLU）处理输入信号，提取非线性特征。
   • 输出层：输出预测结果,可能为分类标签或连续值。

2. 前向传播
   数据从输入层逐层传递至输出层，每一层通过权重矩阵和偏置向量计算输出值：
   $$
   a^{(l)} = f(W^{(l)} cdot a^{(l-1)} + b^{(l)})
   $$
   $f$为激活函数，$W^{(l)}$为第$l$层的权重矩阵，$b^{(l)}$为偏置。

3. 误差反向传播
   通过计算输出层的误差（如均方误差），逐层反向传播误差信号，并更新各层的权重与偏置：

   • 误差计算：使用损失函数（如交叉熵、均方误差）衡量预测值与真实值的差距。
   • 梯度下降：利用链式法则计算权重与偏置的梯度，按学习率调整参数：
     $$
     W{new} = W{old} – eta cdot frac{partial L}{partial W}
     $$
     $eta$为学习率，$L$为损失函数。

BP神经网络的实现步骤

以下是Python中实现BP神经网络的典型流程：

数据预处理

• 对输入数据进行标准化或归一化。
• 分类任务需对标签进行独热编码（One-Hot Encoding）。

from sklearn.preprocessing import StandardScaler, OneHotEncoder
# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
# 标签独热编码
encoder = OneHotEncoder()
y_train = encoder.fit_transform(y_train.reshape(-1, 1)).toarray()

网络参数初始化

• 权重矩阵使用随机初始化（如Xavier方法）,偏置初始化为0。

import numpy as np
def initialize_parameters(input_size, hidden_size, output_size):
    np.random.seed(42)
    W1 = np.random.randn(input_size, hidden_size) * np.sqrt(2. / input_size)
    b1 = np.zeros((1, hidden_size))
    W2 = np.random.randn(hidden_size, output_size) * np.sqrt(2. / hidden_size)
    b2 = np.zeros((1, output_size))
    return {"W1": W1, "b1": b1, "W2": W2, "b2": b2}

前向传播计算

• 激活函数选择：隐含层常用ReLU，输出层用Softmax（分类）或线性函数（回归）。

def forward_propagation(X, parameters):
    W1, b1 = parameters["W1"], parameters["b1"]
    W2, b2 = parameters["W2"], parameters["b2"]
    # 隐含层计算
    Z1 = np.dot(X, W1) + b1
    A1 = np.maximum(0, Z1)  # ReLU激活函数
    # 输出层计算
    Z2 = np.dot(A1, W2) + b2
    A2 = np.exp(Z2) / np.sum(np.exp(Z2), axis=1, keepdims=True)  # Softmax
    return {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2}

反向传播与参数更新

• 计算损失函数的梯度，使用优化算法（如Adam、SGD）更新参数。

def backward_propagation(X, y, parameters, cache, learning_rate=0.01):
    m = X.shape[0]
    W1, W2 = parameters["W1"], parameters["W2"]
    A1, A2 = cache["A1"], cache["A2"]
    # 输出层误差计算
    dZ2 = A2 - y
    dW2 = (1 / m) * np.dot(A1.T, dZ2)
    db2 = (1 / m) * np.sum(dZ2, axis=0, keepdims=True)
    # 隐含层误差计算
    dZ1 = np.dot(dZ2, W2.T) * (A1 > 0)  # ReLU导数
    dW1 = (1 / m) * np.dot(X.T, dZ1)
    db1 = (1 / m) * np.sum(dZ1, axis=0, keepdims=True)
    # 更新参数
    parameters["W1"] -= learning_rate * dW1
    parameters["b1"] -= learning_rate * db1
    parameters["W2"] -= learning_rate * dW2
    parameters["b2"] -= learning_rate * db2
    return parameters

训练与评估

• 设置迭代次数（epoch）和批量大小（batch size）,监控训练损失与准确率。

def train(X, y, epochs=1000, learning_rate=0.01):
    parameters = initialize_parameters(input_size=4, hidden_size=5, output_size=3)
    for epoch in range(epochs):
        cache = forward_propagation(X, parameters)
        loss = -np.mean(y * np.log(cache["A2"] + 1e-8))  # 交叉熵损失
        parameters = backward_propagation(X, y, parameters, cache, learning_rate)
        if epoch % 100 == 0:
            print(f"Epoch {epoch}, Loss: {loss:.4f}")
    return parameters

优化技巧与常见问题

1. 防止过拟合
   • 添加L2正则化项。
   • 使用Dropout随机丢弃部分神经元。
2. 加速收敛
   • 采用自适应学习率算法（如Adam）。
   • 输入数据归一化。
3. 梯度消失/爆炸
   • 使用Batch Normalization（批量归一化）。
   • 更换激活函数（如ReLU替代Sigmoid）。

BP神经网络的应用场景

• 图像识别：手写数字分类（如MNIST数据集）。
• 金融预测：股票价格趋势分析。
• 自然语言处理：文本情感分类。

引用说明 参考以下资料：

1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
2. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
3. 周志华. (2016). 《机器学习》. 清华大学出版社.