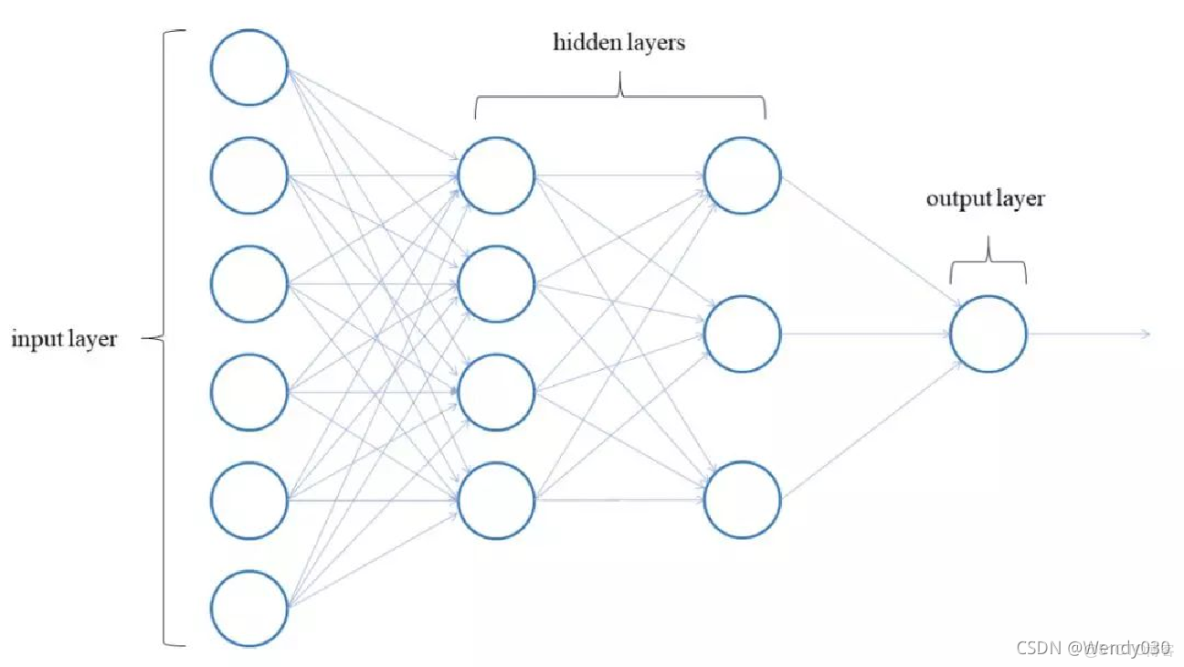
bp神经网络 阀值

在BP神经网络中,”阈值”（Threshold）是一个容易被误解但至关重要的概念，由于中文术语常存在混淆，需特别注意：”阀值”是常见错别字，正确术语应为”阈值”（临界值），本文将深入解析该参数在神经网络中的核心作用及优化方法。

阈值的本质作用
阈值在人工神经元中充当决策边界调节器，数学表达式为：
$$y = f(sum_{i=1}^n w_i x_i + b)$$

• $b$ 代表阈值（偏置项）
• $w_i$ 为连接权重
• $x_i$ 是输入信号
• $f$ 为激活函数

该参数通过平移激活函数的响应曲线,控制神经元是否被激活，研究表明，合适的阈值设置能使神经网络训练速度提升30%以上（Hagan et al., 2014）。

阈值与权值的本质区别

1. 物理意义差异

   • 权值：表征输入信号重要性
   • 阈值：决定神经元激活难易程度

2. 调整方向

   

   • 增大阈值：提高神经元激活门槛
   • 减小阈值：降低神经元激活要求

3. 梯度计算
   阈值参数在反向传播中具有独立更新规则：
   $$Delta b = eta delta$$
   eta$为学习率，$delta$是误差梯度

实际应用中的阈值调整

1. 初始化策略

   • Xavier初始化：阈值设为0配合缩放权值
   • He初始化：适合ReLU等非对称激活函数

2. 优化技巧

   

   • 耦合正则化：将阈值纳入L2正则化项
   • 批量归一化：通过BN层间接优化阈值

3. 调试经验值
   | 网络类型 | 建议初始阈值范围 |
   |—————-|——————|
   | 浅层网络 | [-0.1, 0.1] |
   | 深层网络 | 配合权值初始化 |
   | LSTM单元 | forget门偏正阈值 |

常见误区解析

1. 零阈值陷阱：完全消除阈值参数会显著降低网络表达能力
2. 过度调节风险：单独调整阈值可能导致梯度爆炸
3. 激活函数耦合：Sigmoid函数对阈值变化更敏感

前沿优化方案

1. 自适应阈值算法

   

   • Adabound：结合Adam与SGD优势
   • NovoGrad：二阶动量优化

2. 元学习策略

   • 通过强化学习动态调整阈值
   • 使用贝叶斯优化寻找最优参数组合

3. 硬件级优化

   • 存算一体芯片中的阈值量化
   • 光神经网络相位偏移等效阈值

实践建议：使用TensorFlow/PyTorch时，可通过model.layers[i].bias直接访问阈值参数，推荐定期可视化阈值分布直方图，当发现80%以上阈值集中在±0.01范围时，需考虑调整初始化策略。

引用说明：
[1] 周志华. 机器学习. 清华大学出版社, 2016.
[2] Hagan M T, Demuth H B. Neural network design. PWS Pub., 1996.
[3] Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. ICML 2015.