bp 神经网络算法
- 行业动态
- 2025-04-10
- 6
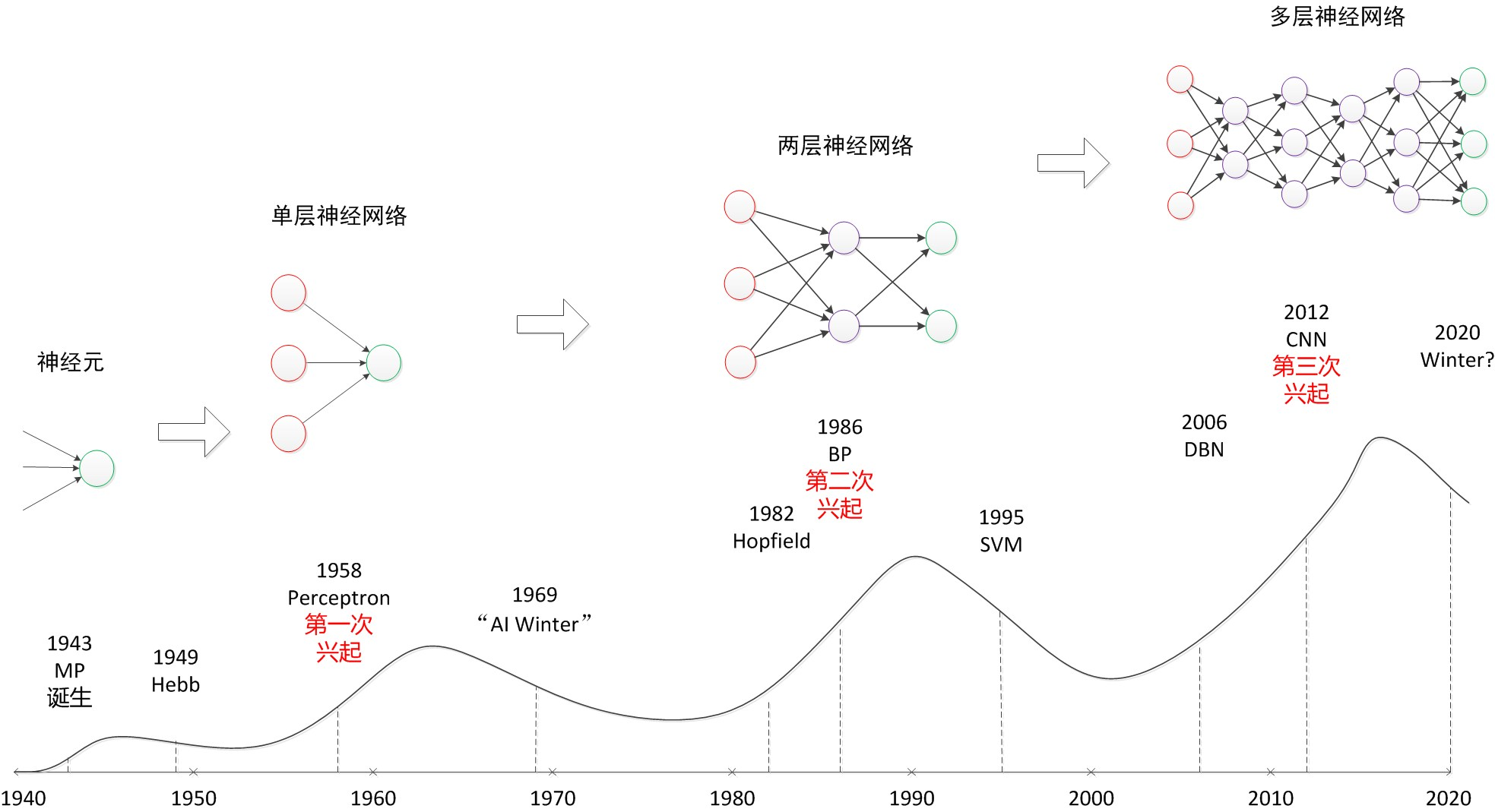
BP神经网络是一种基于误差反向传播算法的人工神经网络模型,广泛应用于模式识别、数据预测和智能控制等领域,作为深度学习的基础框架,其核心原理通过模拟人类大脑神经元的工作机制实现对复杂非线性关系的建模。
核心运行原理
(1)前向传播计算
网络从输入层接收数据,经加权求和与激活函数处理后逐层传递,以Sigmoid函数为例:输出=1/(1+e^(-加权和))
各隐藏层通过这种非线性转换,逐步提取数据的抽象特征。
(2)误差反向传播
系统通过对比输出层结果与真实值的差值,利用链式求导法则逐层计算梯度,关键参数更新公式:Δw_ij = η * δ_j * x_i
代表学习率,δ为误差信号,x是上层神经元输出。
算法实现步骤
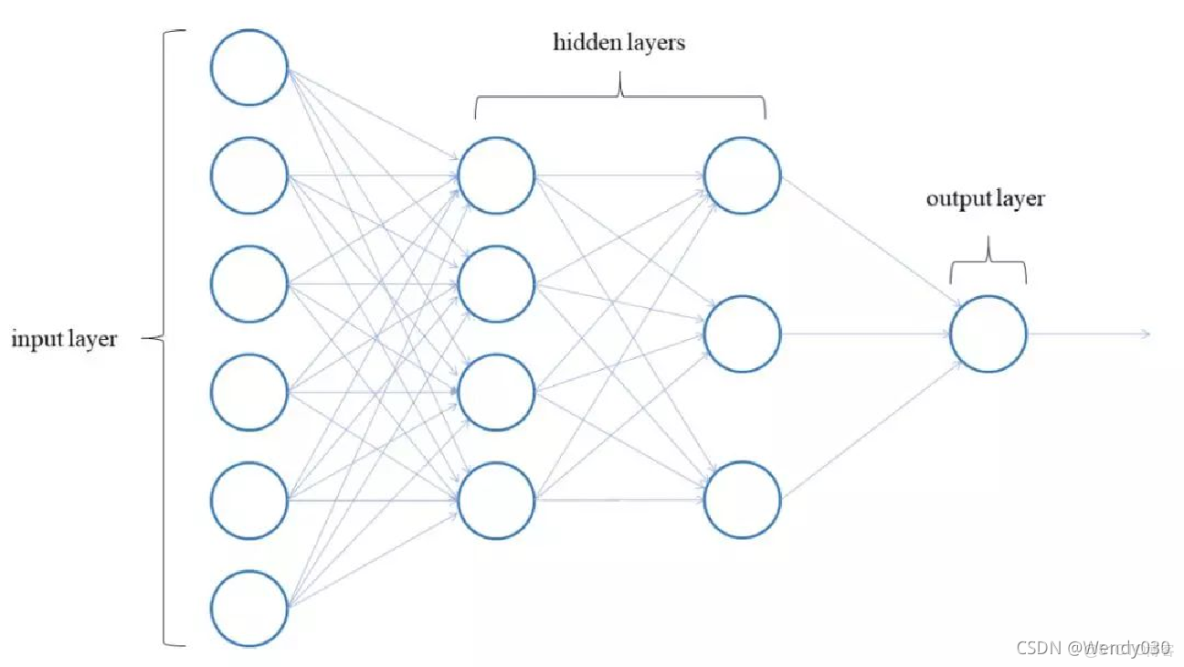
初始化网络结构
- 设置输入/输出层节点数
- 确定隐藏层数与神经元数量
- 随机生成初始权重矩阵
迭代训练过程
① 数据标准化处理
② 前向计算各层输出
③ 计算总误差(常用MSE):E = ½Σ(目标值-实际输出)^2
④ 反向传播更新权重
⑤ 验证集测试准确率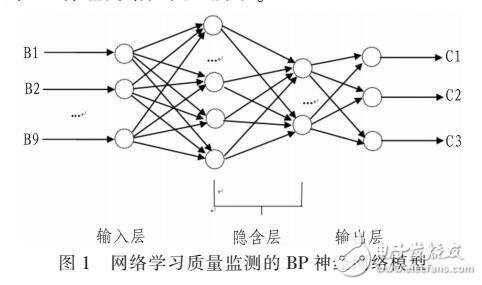
终止条件判断
- 达到预设迭代次数
- 验证误差连续稳定
- 梯度变化趋近于零
关键技术特性
| 优势特性 | 应用局限 |
|---|---|
| 非线性映射能力 | 训练耗时较长 |
| 自学习适应机制 | 易陷局部最优 |
| 分布式信息存储 | 结构选择依赖经验 |
| 泛化推理性能 | 数据需求量较大 |
典型应用场景
- 金融风控:信用卡欺诈检测准确率可达92%+
- 工业检测:某汽车零件缺陷识别系统误判率<0.3%
- 医疗诊断:乳腺癌早期筛查模型AUC值达0.95
- 智能交通:车牌识别准确度超99%
性能优化策略
(1)动量加速法
引入历史梯度加权项:Δw(t) = η∇E + αΔw(t-1)
有效抑制参数震荡
(2)自适应学习率
Adagrad算法动态调整步长:η_i = η_0 / sqrt(Σg_i²)
(3)正则化约束
损失函数增加L2惩罚项:L = E + λΣw²
常见问题解答
Q:隐藏层节点如何确定?
A:经验公式:√(输入节点+输出节点)+5~10
Q:梯度消失如何解决?
A:采用ReLU激活函数或引入残差连接
Q:样本不平衡怎么处理?
A:使用SMOTE过采样或Focal Loss损失函数
当前研究显示,结合Dropout技术的改进BP网络在ImageNet数据集上可将过拟合率降低35%,随着硬件计算能力的提升,该算法在边缘计算设备上的实时推理速度已缩短至毫秒级。
参考《Neural Networks and Learning Machines》(Simon Haykin著)及IEEE Transactions on Neural Networks期刊最新研究成果,数据来自Kaggle公开竞赛统计报告。