伴随矩阵是什么

伴随矩阵（Adjoint matrix）是线性代数中的一个概念，它与一个方阵的行列式和特征值有关，伴随矩阵的定义如下：

1、定义：对于一个n阶方阵A，其伴随矩阵记作adj(A)或A*。

2、性质：

adj(A)是一个n阶方阵；

adj(A)的行数和列数与A相同；

adj(A)的每个元素a_ij等于A的每个元素的代数余子式（即去掉第i行第j列的元素后得到的行列式的值）。

3、计算方法：

对于2阶方阵A，其伴随矩阵为：

“`

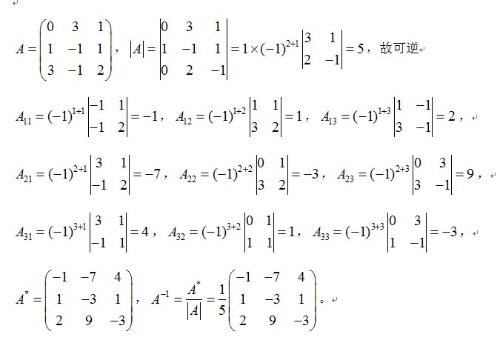
A = | a b |

| c d |

adj(A) = | ad bc |

| bd ac |

“`

对于3阶方阵A，其伴随矩阵为：

“`

A = | a b c |

| d e f |

| g h i |

adj(A) = | aei +bfg +cdi acef bdfg cdeh |

| chf adi beh cfg |

| afg bdh cei |

“`

对于n阶方阵A，其伴随矩阵的计算方法类似，需要计算每个元素的代数余子式。

4、伴随矩阵的性质：

(adj(A))’ = A；

(adj(kA)) = k^n * adj(A)，其中k为常数；

det(A) = (1)^(n+1) * det(adj(A))。