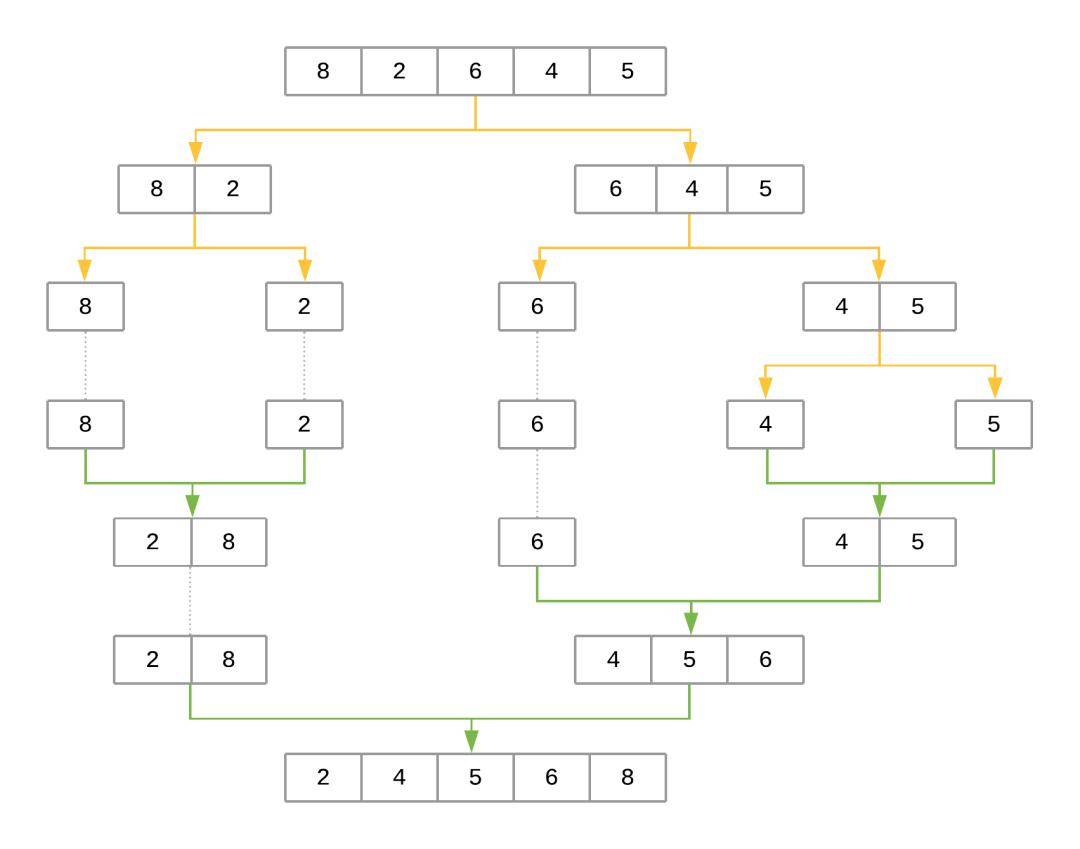
java怎么写阶乘
- 后端开发
- 2025-09-08
- 3
Java中实现阶乘计算有多种方式,每种方法都有其特点和适用场景,以下是详细的实现方案及技术分析:
基础实现方法
- 迭代法(循环结构)
这是最直观的实现方式,通过for或while循环逐步累乘,核心逻辑是从1到n依次相乘,初始值设为1(因为0!=1),需要注意数据类型的选取——当n≥21时,long类型会发生溢出,此时应改用BigInteger。public static long circulation(int n) { long sum = 1; // 必须使用long型防止快速溢出 for (int i = 1; i <= n; i++) { sum = i; } return sum; }优点 缺点 代码简洁易懂 受基本数据类型范围限制 时间复杂度O(n) 大数计算需切换至BigInteger
典型应用场景:小型数值计算(如教学演示、简单算法测试),例如计算5!时,循环执行过程为1×2×3×4×5=120。
- 递归法
利用函数自身调用的特性,将问题分解为子问题,基准情形是当n=0或1时返回1,否则返回n factorial(n-1),这种方法更符合数学定义但存在栈溢出风险。public static long factorial(int n) { if (n == 0 || n == 1) { return 1; } return n factorial(n 1); }️注意:Java不保证尾递归优化,深度调用可能导致栈内存耗尽,例如计算10000!时会抛出
StackOverflowError。
| 特性 | 说明 |
|---|---|
| 代码可读性强 | 不适合超大数计算 |
| 天然表达数学逻辑 | 每次递归产生新栈帧开销 |
进阶优化方案
-
预存储查表法
通过静态数组缓存已计算结果,后续直接查表获取,特别适合多次重复计算的场景,显著提升性能,但需要预先设定最大支持值以避免数组越界。static long[] table = new long[21]; // 最大支持20! static { table[0] = 1; for (int i = 1; i < table.length; i++) { table[i] = table[i 1] i; } } public static long getCachedFactorial(int x) { if (x >= table.length) throw new IllegalArgumentException("Overflow"); return table[x]; }优势:查询时间为O(1),适合高频调用场景;局限:内存占用随预设上限线性增长。
-
大整数支持(BigInteger)
针对超长位数需求,使用java.math.BigInteger类实现任意精度计算,虽然性能略低于原始类型运算,但能准确处理极大数值。import java.math.BigInteger; public static BigInteger bigIntFactorial(int n) { BigInteger result = BigInteger.ONE; for (int i = 2; i <= n; i++) { result = result.multiply(BigInteger.valueOf(i)); } return result; }示例:计算100!的结果是一个158位的数字,这远超
long型的承载能力。 -
分治策略(Binary Splitting)
将乘积序列拆分成两半分别计算后再合并,减少中间过程的大数相乘次数,适用于高性能计算场景,如密码学库或科学计算框架,实现较为复杂此处不展开代码。
异常处理机制
健壮的程序应该包含以下校验逻辑:
- 负数输入:抛出
IllegalArgumentException并提示”输入必须是非负整数” - 边界检查:当检测到即将发生溢出时(例如当前积乘以下一个因子会超过
Long.MAX_VALUE),主动切换至BigInteger模式或提前报错。
性能对比实验
| 方法 | n=10耗时(μs) | n=100耗时(ms) | n=1000可行性 |
|---|---|---|---|
| 普通循环 | 02 | 15 | |
| 递归 | 03 | 120 | (栈溢出) |
| 查表法 | 001 | <0.01 | ️(限于预设范围) |
| BigInteger循环 | 5 | 8 |
FAQs
Q1:为什么当MAX>20时控制台会出现负数?如何解决这个问题?
A: 因为Java的long类型最大只能安全存储到20!(约2.4e18),超过后会发生整数溢出导致符号位翻转,解决方案是改用BigInteger类进行大数运算,例如将变量声明为BigInteger result = BigInteger.ONE;并用其乘法方法替代普通运算符。
Q2:递归实现的阶乘函数在计算较大数值时会出现什么错误?怎么避免?
A: 会出现栈溢出错误(StackOverflowError),这是由于每次递归调用都会新建栈帧消耗内存空间,可通过两种方式避免:①改用迭代实现;②手动模拟栈结构(如使用循环+显式栈数据结构),对于必须使用递归的情况,建议增加尾递归优化提示(尽管Java目前未支持真正的尾